Advanced: Learning a Gurobi Model from DataGet Started
What is Mathematical Optimization?
Mathematical optimization is the process of finding the best solution to a problem defined by an objective function and constraints. A common example is maximizing profits in a factory’s production schedule or minimizing travel distances in a delivery network. It translates real-world scenarios into mathematical models that seek maximum or minimum values. Constraints encapsulate practical or theoretical limitations, guiding the feasible solution space.
What is Gurobi?
Gurobi (www.gurobi.com) is a leading solver for advanced mathematical optimization problems. It leverages efficient algorithms and parallel computing to handle large-scale models at high speed. Widely adopted across industries, Gurobi empowers organizations to make data-driven decisions and achieve cost savings.
What is Causara?
Causara is a Python package that converts ANY objective function into an exact, approximative or surrogate Gurobi model using AI and sophisticated new machine learning algorithms. You can also provide both: an already existing Gurobi model and (a more detailed) objective function. causara will then fine-tune the Gurobi model to close the gap between model and objective function. Additionally we have developed an intuitive GUI for running Gurobi models by non-technical staff.
Installation
Start by installing the Causara package via pip
pip install causara
Next, generate a test key. You will receive it via email:
python
>>> import causara
>>> causara.create_key("my_mail@xxx")
Quickstart
This guide demonstrates how to use Causara to compile and solve any optimization problem. Every optimization problem can be expressed as:
where:
- p represents the problem variables (inputs).
- c represents the constant data (fixed parameters).
- x represents the decision variables.
Overview of the Demo:
The main class in Causara is CompiledGurobiModel. You can compile a model from a Python objective function
(and an additional Gurobi model) using the compile(.) method. The Python objective function must always have three input parameters:
p, c and x. They are dicts and contain the problem variables, constants and decision variables respectively.
Keys in these dicts are always strings and values are ints, floats or numpy arrays. In addition to the objective function you must provide a function
that returns a DecisionVars object where you define the deicion variables including their type (binary, integer, continuous), their shape (number of variables),
as well as lower and upper bounds.
Objective function:
We now want to compile the following objective function. The function must return a float as an objective value, constraints can be defined using assert statements. You can use any calculation you want in this function to compute the objective value.
def simple_demo(p, c, x):
coef = p["coef"]
var = x["var"]
assert var[0] < var[1] and np.sum(var) == 10
return coef * var[0] + var[0] * var[1]
Decision variables function:
Next, we need to define the decision variables, including their names, types, shapes and bounds.
def get_decision_vars(p, c):
decision_vars = DecisionVars()
# Here we create two integer variables with name "var" and bounds [-10,+10]
decision_vars.add_integer_vars("var", 2, minimum=-10, maximum=+10)
return decision_vars
Complete Demo Code:
Note: you must insert your own key into the code below
from causara import *
from gurobipy import GRB
import numpy as np
def simple_demo(p, c, x):
coef = p["coef"]
var = x["var"]
assert var[0] < var[1] and np.sum(var) == 10
return coef * var[0] + var[0] * var[1]
def get_decision_vars(p, c):
decision_vars = DecisionVars()
# Here we create two integer variables with name "var" and bounds [-10,+10]
decision_vars.add_integer_vars("var", 2, minimum=-10, maximum=+10)
return decision_vars
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="demo") # insert your key here and provide a model name
compiledGurobiModel.compile(decision_vars_func=get_decision_vars, # the decision_vars_func
real_func=simple_demo, # the objective function
P_val=[{"coef": 1.0}], # a list of problems p for validating the correctness
sense=GRB.MINIMIZE) # the sense (either GRB.MINIMIZE or GRB.MAXIMIZE)
# After compiling we can solve a new problem instance p={"coef": 1.5}
data = compiledGurobiModel.solve(p={"coef": 1.5}) # Return value of the solve(.) method is an object of type Data
print(f"Optimal x: {data.list_of_x[0]}")
print(f"Optimal value: {data.gurobi_values[0]}")
Demo 1: n-agent TSP
The n-agent Traveling Salesman Problem (TSP) extends the classic TSP to multiple agents. In this formulation, n agents are assigned routes so that every city is visited by at least one agent. All agents start and end their routes at the same designated city (commonly city 0). The goal is to minimize the maximum route length (or travel time) among all agents, ensuring that no single agent is overburdened and that the overall completion time is optimized.
As decision variables we need a 2d numpy array named "routes". One row for each city-position. One column for each agent. The number therefore represents to city-ID, so we have bounds [0, num_cities-1].
We start by defining the objective function using plain Python:
def n_agent_TSP(p, c, x):
distances = p["distances"]
num_cities = p["num_cities"]
num_agents = p["num_agents"]
routes = x["routes"] # routes is a 2d numpy array. One row for each city-position. One column for each agent.
assert equal(routes[0], 0) # all agents start at city 0
assert equal(routes[num_cities-1], 0) # all agents end at city 0
for city_nr in range(num_cities):
assert city_nr in routes # assert that every city is visited by at least one agent
path_lengths = [0] * num_agents
for agent_nr in range(num_agents):
for position_nr in range(num_cities-1):
city_nr = int(routes[position_nr][agent_nr])
next_city_nr = int(routes[position_nr + 1][agent_nr])
path_lengths[agent_nr] += distances[city_nr][next_city_nr]
cost = max(path_lengths) # cost = maximum distance that any of the agents needs to travel
return cost
Next, we define the decision variables of this optimization problem (all variables x that are used in the objective function).
def get_decision_vars(p, c):
num_cities = p["num_cities"]
num_agents = p["num_agents"]
decision_vars = DecisionVars()
# routes is a 2d numpy array. One row for each city-position. One column for each agent.
# The number represents to city-ID, so we have bounds [0, num_cities-1]
decision_vars.add_integer_vars(name="routes",
shape=(num_cities, num_agents),
minimum=0,
maximum=num_cities-1)
return decision_vars
Complete Code
from causara import *
from gurobipy import GRB
def n_agent_TSP(p, c, x):
distances = p["distances"]
num_cities = p["num_cities"]
num_agents = p["num_agents"]
routes = x["routes"] # routes is a 2d numpy array. One row for each city-position. One column for each agent.
assert equal(routes[0], 0) # all agents start at city 0
assert equal(routes[num_cities-1], 0) # all agents end at city 0
for city_nr in range(num_cities):
assert city_nr in routes # assert that every city is visited by at least one agent
path_lengths = [0] * num_agents
for agent_nr in range(num_agents):
for position_nr in range(num_cities-1):
city_nr = int(routes[position_nr][agent_nr])
next_city_nr = int(routes[position_nr + 1][agent_nr])
path_lengths[agent_nr] += distances[city_nr][next_city_nr]
cost = max(path_lengths) # cost = maximum distance that any of the agents needs to travel
return cost
def get_decision_vars(p, c):
num_cities = p["num_cities"]
num_agents = p["num_agents"]
decision_vars = DecisionVars()
# routes is a 2d numpy array. One row for each city-position. One column for each agent.
# The number represents to city-ID, so we have bounds [0, num_cities-1]
decision_vars.add_integer_vars(name="routes",
shape=(num_cities, num_agents),
minimum=0,
maximum=num_cities-1)
return decision_vars
# create 3 random problem instances for validating the correctness of the Gurobi model
P_val = Demos.n_agent_TSP.generate_P(3, num_cities=15, num_agents=3)
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="n_agent_TSP")
compiledGurobiModel.compile(decision_vars_func=get_decision_vars,
real_func=n_agent_TSP,
sense=GRB.MINIMIZE,
P_val=P_val)
p = P_val.iloc[0]
data = compiledGurobiModel.solve(p)
print(data.list_of_x[0])
Demo 2: Cell-Tower Placement
In many real-world optimization problems, it is extremely challenging to capture every nuance or detail in the mathematical formulation. Gurobi models are often simplified representations that approximate the original problem. Consequently, some real-world constraints or objectives might be only loosely modeled. Causara comes with a solution to this problem: fine-tuning an existing Gurobi model to close the gap between model and real-world objective function.
For instance, in the following cell tower placement demo, the Gurobi model uses simplifying assumptions. Subsequently causara fine-tunes the model.
In this demo, we are given a map that specifies the desired cell coverage over an area. Our goal is to decide where to place cell towers such that the desired coverage is achieved. This optimization problem is very complex and difficult to optimize, so we make two key simplifying assumptions:
First Simplification: We assume that the cell coverage of a tower is a rectangle around the tower rather than a circle. Although in reality the coverage is circular, using a rectangular approximation simplifies the constraints and makes the problem more tractable.
Second Simplification: We coarsen the resolution of the coverage map. Instead of working with a very fine grid that represents the real area, we aggregate cells into larger “coarse” cells. This reduces the problem size and further simplifies the model. The number 0, 1, 2, ... represents the number of cell towers that should be reachable from this cell.
Using these adjustments, we can formulate a Gurobi model that ensures each coarse cell receives at least the desired amount of coverage. However, because these assumptions are simplifications, the solution from the Gurobi model may not perfectly meet the original high-resolution and circular coverage requirements.
The real-world objective function is to minimize the number of cell with insufficient coverage:
def real(p, c, x):
desired_coverage = p["desired_coverage"]
size = int(p["size"])
cell_towers = x["cell_towers"]
# Calculate tower positions in the finer resolution (10x finer than the coarse resolution)
fine_size = size * 10
tower_positions = []
for i in range(size):
for j in range(size):
if cell_towers[i][j] == 1:
tower_positions.append((i * 10 + 5, j * 10 + 5)) # Center of the coarse cell (i, j) in the fine grid
# Calculate coverage in the finer resolution with circles instead of squares
coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
for tower_x, tower_y in tower_positions:
distance = np.sqrt((i - tower_x)**2 + (j - tower_y)**2)
if distance <= 40: # Radius of 40 in the fine grid corresponds to 4 in coarse grid
coverage[i][j] += 1
# Calculate the number of cells for which the coverage does not meet the desired coverage
insufficient_cell_coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
if coverage[i][j] < desired_coverage[i][j]:
insufficient_cell_coverage[i][j] = 1
return np.sum(insufficient_cell_coverage)
The Gurobi model with the simplifying assumptions is:
def gurobi(p, c):
desired_coverage_coarse = p["desired_coverage_coarse"]
size = p["size"]
model = gp.Model()
cell_towers = model.addVars(size, size, vtype=GRB.BINARY, name='cell_towers')
coverage = model.addVars(size, size, vtype=GRB.INTEGER, name='coverage') # number of cell towers reachable from this cell
# Coverage for cell (i, j) = the number of towers in the square neighborhood with radius 3
for i in range(size):
for j in range(size):
neighborhood = [cell_towers[k, l]
for k in range(max(0, i-3), min(size, i+3+1))
for l in range(max(0, j-3), min(size, j+3+1))]
model.addConstr(coverage[i, j] == gp.quicksum(neighborhood), name=f"coverage_{i}_{j}")
# Enforce desired coverage constraints
for i in range(size):
for j in range(size):
model.addConstr(coverage[i, j] >= desired_coverage_coarse[i][j], name=f"min_cov_{i}_{j}")
model.addConstr(gp.quicksum(cell_towers) == 9)
model.setObjective(0, GRB.MINIMIZE)
return model
We can now pass both functions to causara and it will fine-tune the Gurobi model on the more detailed real-world objective function.
Complete Code
from causara import *
import causara
import gurobipy as gp
from gurobipy import GRB
import numpy as np
def real(p, c, x):
desired_coverage = p["desired_coverage"]
size = int(p["size"])
cell_towers = x["cell_towers"]
# Calculate tower positions in the finer resolution (10x finer than the coarse resolution)
fine_size = size * 10
tower_positions = []
for i in range(size):
for j in range(size):
if cell_towers[i][j] == 1:
tower_positions.append((i * 10 + 5, j * 10 + 5)) # Center of the coarse cell (i, j) in the fine grid
# Calculate coverage in the finer resolution with circles instead of squares
coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
for tower_x, tower_y in tower_positions:
distance = np.sqrt((i - tower_x)**2 + (j - tower_y)**2)
if distance <= 40: # Radius of 40 in the fine grid corresponds to 4 in coarse grid
coverage[i][j] += 1
# Calculate the number of cells for which the coverage does not meet the desired coverage
insufficient_cell_coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
if coverage[i][j] < desired_coverage[i][j]:
insufficient_cell_coverage[i][j] = 1
return np.sum(insufficient_cell_coverage)
def gurobi(p, c):
desired_coverage_coarse = p["desired_coverage_coarse"]
size = p["size"]
model = gp.Model()
cell_towers = model.addVars(size, size, vtype=GRB.BINARY, name='cell_towers')
coverage = model.addVars(size, size, vtype=GRB.INTEGER, name='coverage') # number of cell towers reachable from this cell
# Coverage for cell (i, j) = the number of towers in the square neighborhood with radius 3
for i in range(size):
for j in range(size):
neighborhood = [cell_towers[k, l]
for k in range(max(0, i-3), min(size, i+3+1))
for l in range(max(0, j-3), min(size, j+3+1))]
model.addConstr(coverage[i, j] == gp.quicksum(neighborhood), name=f"coverage_{i}_{j}")
# Enforce desired coverage constraints
for i in range(size):
for j in range(size):
model.addConstr(coverage[i, j] >= desired_coverage_coarse[i][j], name=f"min_cov_{i}_{j}")
model.addConstr(gp.quicksum(cell_towers) == 9)
model.setObjective(0, GRB.MINIMIZE)
return model
def get_decision_vars(p, c):
size = p["size"]
decision_vars = DecisionVars()
decision_vars.add_binary_vars("cell_towers", (size, size))
return decision_vars
def evaluate(compiledGurobiModel, P_test):
insufficient_cell_coverage = []
for i in range(20):
p = P_test.iloc[i]
data = compiledGurobiModel.solve(p, num_solutions=3)
x = data.get_list_of_x()[0] # choose the best solution according to the current model
insufficient_cell_coverage.append(real(p, {}, x))
return float(np.mean(insufficient_cell_coverage))
P_val = causara.Demos.Cell_tower.generate_P(n=120, size=10)
P_test = causara.Demos.Cell_tower.generate_P(n=20, size=10)
params = {'nHiddens': [64, 64, 64], 'nEpochs': 30, 'val_freq': 10}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="cell_towers")
compiledGurobiModel.compile(decision_vars_func=get_decision_vars,
real_func=real,
gurobi_func=gurobi,
P_val=P_val,
sense=GRB.MINIMIZE,
num_evaluations_per_p=3,
num_iterations=4,
time_limit=10,
p_vars_finetuning=["desired_coverage_coarse"],
params=params)
print("Evaluation P_val: ", evaluate(compiledGurobiModel, P_val))
print("Evaluation P_test: ", evaluate(compiledGurobiModel, P_test))
Advanced: Learning a Gurobi Model from Data
As introduced in the Quickstart section, every optimization problem can be formulated as:
x* = argmax f(p, c, x)
where:
- p represents the problem variables (inputs).
- c represents the constant data (fixed parameters).
- x represents the decision variables.
We now want to learn this function f that encodes this optimization problem given a set of training data [(p,x*)].
We therefore don't need to know how to encode an optimization problem with Gurobi.
compile_from_data(get_decision_vars, P, X, P_val, X_val, params)
get_decision_vars: The decision variablesP: A pandas DataFrame or a list of dictsX: A pandas DataFrame or a list of dictsP_val(optional): Validation input data. A pandas DataFrame or a list of dictsX_val(optional): Validation output data. A pandas DataFrame or a list of dictsparams: A dictionary of hyperparameters that configure the neural network
In the following we will present two demos on how to use this feature.
Predicting Molecules with a Specified Property Vector
In this section, we demonstrate how to learn a Gurobi model which can predict a molecule that has a specified property vector.
We use the QM9 dataset, a collection of small organic molecules from quantum chemistry simulations, to illustrate this process.
QM9 provides computed molecular properties, such as dipole moments or polarizabilities, making it well-suited for tasks like ours.
In the mathematical framework x* = argmax f(p, c, x); p is the property vector (8 dimensions),
c is empty, x is the molecule and f is the Gurobi model we want to learn.
1. Reading and Preparing the Dataset
We use the QM9 dataset, which is distributed as a compressed file named dsgdb9nsd.xyz.tar.bz2. A direct download link is available from https://figshare.com/ndownloader/files/3195389. You can also use this command to download the dataset:
wget --no-check-certificate -O dsgdb9nsd.xyz.tar.bz2 "https://figshare.com/ndownloader/files/3195389"This dataset contains:
- properties: For each molecule, we have a vector of numerical values describing different physical/chemical properties (e.g., dipole moment, HOMO-LUMO gap).
- molecules: Molecules are represented in SMILES notation. For learning a Gurobi model we need
xto be a binary vector. We could directly represent the molecule as a graph, but we decided to use binary fingerprints in this demo since it is more compact. We used the MACCS fingerprints
from rdkit import RDLogger
RDLogger.DisableLog('rdApp.*')
import numpy as np
from causara import *
import matplotlib.pyplot as plt
from causara.Demos.MoleculePrediction import read_dsg_dataset
dataset_file = "/path/to/dsgdb9nsd.xyz.tar.bz2"
properties, fingerprints = read_dsg_dataset(dataset_file)
print(f"\nproperties.shape: {properties.shape}")
print(f"fingerprints.shape: {fingerprints.shape}\n")
2. Visualizing the Data
We can now plot the distribution of each molecular property.
def plot_data(properties, fingerprints):
import matplotlib
matplotlib.use("TkAgg")
# Plot distribution for every feature in normalized_properties
num_features = properties.shape[1]
fig, axes = plt.subplots(4, 2, figsize=(16, 12)) # Create a 4x2 grid
axes = axes.flatten() # Flatten the 2D array of axes to 1D for easier iteration
labels = [
"Dipole moment",
"Isotropic polarizability",
"Energy of Highest occupied molecular orbital (HOMO)",
"Energy of Lowest occupied molecular orbital (LUMO)",
"Gap, difference between LUMO and HOMO",
"Electronic spatial extent",
"Zero point vibrational energy",
"Internal energy at 0 K"
]
for i in range(num_features):
axes[i].hist(properties[:, i], bins=100, color='skyblue', edgecolor='black', alpha=0.7)
axes[i].set_title(labels[i])
axes[i].set_xlabel('Normalized Value')
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
matplotlib.use("Agg")
plot_data(properties, fingerprints)
3. Splitting the Dataset into Training and Test Subsets
After loading the dataset, we partition it into two parts:
- properties_train, fingerprints_train: Used to train or compile the Gurobi model.
- properties_test, fingerprints_test: Used to evaluate the model's performance by comparing predictions against real molecular data.
properties_train = properties[:40000]
fingerprints_train = fingerprints[:40000]
properties_test = properties[40000:]
fingerprints_test = fingerprints[40000:]
4. Compiling the Model from Data
We call compile_from_data() on our CompiledGurobiModel object to create a Gurobi model f(p,x)
such that for every (p,x) pair it holds that the molecule x is the optimal solution when faced with the property vector p.
5. Evaluating the Model
Once compiled, we use the evaluate() function to test the model on unseen data. The process is:
- Randomly choose a
target_propertyvector fromproperties_test. - Compute the objective value for all molecules in the test set to see how well each candidate matches the target property.
- Identify the top candidates and measure how close their properties are to the target (using an absolute distance metric).
- Report the best match among these top candidates and provide its rank if we sorted all molecules by their distance to the target.
Complete Code
Below is the entire code, putting together all of the above steps. Adjust the dataset_file path according to where you have placed
dsgdb9nsd.xyz.tar.bz2 and insert your TEST-key.
from rdkit import RDLogger
RDLogger.DisableLog('rdApp.*')
import numpy as np
from causara import *
import matplotlib.pyplot as plt
from causara.Demos.MoleculePrediction import read_dsg_dataset
def plot_data(properties, fingerprints):
import matplotlib
matplotlib.use("TkAgg")
# Plot distribution for every feature in normalized_properties
num_features = properties.shape[1]
fig, axes = plt.subplots(4, 2, figsize=(16, 12)) # Create a 4x2 grid
axes = axes.flatten() # Flatten the 2D array of axes to 1D for easier iteration
labels = [
"Dipole moment",
"Isotropic polarizability",
"Energy of Highest occupied molecular orbital (HOMO)",
"Energy of Lowest occupied molecular orbital (LUMO)",
"Gap, difference between LUMO and HOMO",
"Electronic spatial extent",
"Zero point vibrational energy",
"Internal energy at 0 K"
]
for i in range(num_features):
axes[i].hist(properties[:, i], bins=100, color='skyblue', edgecolor='black', alpha=0.7)
axes[i].set_title(labels[i])
axes[i].set_xlabel('Normalized Value')
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
matplotlib.use("Agg")
def evaluate(compiledGurobiModel, properties_test, fingerprints_test, num_tests=10):
"""
Evaluates the model's performance by:
1. Selecting a random target property vector
2. Retrieving objective values for all test molecules
3. Identifying top molecules according to the objective
4. Computing the absolute distance in property space
5. Determining the best match and its overall rank
"""
print("\n" + "=" * 50 + "\n" + "=" * 50 + "\n")
print("Evaluation Phase")
print("\n" + "=" * 50 + "\n" + "=" * 50 + "\n")
print(f"Number of candidate molecules: {len(properties_test)}\n")
for test in range(num_tests):
# 1. Select a random target property vector
target_property = properties_test[np.random.choice(len(properties_test))]
# 2. Retrieve objective values for all test molecules
obj_values = compiledGurobiModel.get_obj_values({"properties": target_property}, {"fingerprints": fingerprints_test})
# 3. Identify the top 10 candidates (largest objective values)
top10_indices = np.argsort(obj_values)[::-1][:10]
# 4. Compute absolute property distance for these top 10 candidates
top10_abs_dists = []
for i in range(10):
idx = top10_indices[i]
dist = np.sum(np.abs(properties_test[idx] - target_property))
top10_abs_dists.append(dist)
best_among_top10_idx = top10_indices[np.argmin(top10_abs_dists)]
best_abs_distance = np.min(top10_abs_dists)
# Calculate absolute distances for all molecules to find the rank of the best candidate
abs_dists = np.sum(np.abs(properties_test - target_property), axis=1)
sorted_indices = np.argsort(abs_dists) # ascending order
best_rank = np.where(sorted_indices == best_among_top10_idx)[0][0] + 1
# 5. Output results
print(f"Test {test + 1}")
print("Target molecule property: ", [float(f"{value:.3f}") for value in target_property])
print("Property of predicted molecule: ", [float(f"{value:.3f}") for value in properties_test[best_among_top10_idx]])
print(f"Absolute distance between target property and predicted molecule: {best_abs_distance:.3f}")
print(f"Rank in absolute-distance ordering: {best_rank} out of {len(abs_dists)}")
print("\n" + "-" * 50 + "\n")
def get_decision_vars(p, c):
decision_vars = DecisionVars()
decision_vars.add_binary_vars("fingerprints", 167)
return decision_vars
# Download the QM9 dataset from the link below and place it on your system
dataset_file = "/path/to/dsgdb9nsd.xyz.tar.bz2"
properties, fingerprints = read_dsg_dataset(dataset_file)
print(f"\nproperties.shape: {properties.shape}")
print(f"fingerprints.shape: {fingerprints.shape}\n")
# Visualize the data
plot_data(properties, fingerprints)
properties_train = properties[:40000]
fingerprints_train = fingerprints[:40000]
properties_test = properties[40000:]
fingerprints_test = fingerprints[40000:]
params = {
'nHiddens': [128, 128, 128, 256],
'batchSize': 500,
'lr': 0.0013,
'solving_time': 0.5,
'train_val_split': 0.998,
'nEpochs': 100,
'val_freq': 50,
'intraBatchOptimization': False,
'buffer': 0.01
}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Molecule")
compiledGurobiModel.compile_from_data(
get_decision_vars,
P={"properties": properties_train},
X={"fingerprints": fingerprints_train},
params=params)
evaluate(compiledGurobiModel, properties_test, fingerprints_test)
Predicting a Graph with a Specified Distance Matrix
Let G = (V, E) be a graph, where V is the set of vertices and E is the set of edges. Given any graph, it is straightforward to compute the shortest path distance between every pair of vertices; the result is a distance matrix D.
However, the inverse problem—predicting a graph that corresponds to a specified distance matrix—is highly challenging. This is because the problem is inherently a bilevel optimization problem. At the upper level, we seek a graph whose induced distance matrix closely matches the target distance matrix. At the lower level, the graph must satisfy combinatorial constraints (e.g., connectivity, edge existence), and the distances are computed based on the graph structure. These two levels are interdependent, making the overall problem difficult to solve directly.
We want to learn a Gurobi model that predicts a graph for a specified distance matrix:
In this demo, we leverage the fact that computing the distance matrix from a given graph is relatively simple. We generate large amounts of synthetic training data by creating random graphs and computing their corresponding distance matrices. The objective is to train a model that, when presented with a target distance matrix (p), outputs a graph (x) that satisfies the desired distance constraints.
from causara import *
from causara.Demos.DistanceMatrix import generate_data, get_distance_matrix, get_adj_matrix
print("Creating synthetic training data")
P_train, X_train = generate_data(n=7000, size=20)
P_test, X_test = generate_data(n=50, size=20)
We then define an objective function. Note: this objective function is used only for validation. It returns 0 if the predicted graph is correct (i.e. the computed distance matrix for the predicted graph exactly matches the specified distance matrix) and 1 otherwise.
def obj_function(p, x, x_pred):
adj_matrix = get_adj_matrix(x_pred["X"])
distance_matrix_pred = get_distance_matrix(adj_matrix)
if p["P"].shape == distance_matrix_pred.shape and equal(p["P"], distance_matrix_pred):
return 0
else:
return 1
Finally, we train the Gurobi model using the method compile_from_data().
Complete Code
from causara import *
from causara.Demos.DistanceMatrix import generate_data, get_distance_matrix, get_adj_matrix
def evaluate(compiledGurobiModel, P_test, X_test):
numCorrect = 0
for i in range(len(P_test)):
p = P_test.iloc[i]
x = X_test.iloc[i]
data = compiledGurobiModel.solve(p, gurobi_params={"TimeLimit": 0.5}, use_gurobi=True)
if equal(data.list_of_x[0]["X"], x["X"]):
numCorrect += 1
print(f"Result: {numCorrect} / {len(P_test)} correct")
def obj_function(p, x, x_pred):
adj_matrix = get_adj_matrix(x_pred["X"])
distance_matrix_pred = get_distance_matrix(adj_matrix)
if p["P"].shape == distance_matrix_pred.shape and equal(p["P"], distance_matrix_pred):
return 0
else:
return 1
def get_decision_vars(p, c):
decision_vars = DecisionVars()
decision_vars.add_binary_vars("X", 190)
return decision_vars
print("Creating synthetic training data")
P_train, X_train = generate_data(n=7000, size=20)
P_test, X_test = generate_data(n=50, size=20)
params = {
'num_reasoning_cycles': 2,
'nHiddens': [256, 256, 512],
'batchSize': 500,
'lr': 0.0013,
'output_type': 'binary',
'solving_time': 0.1,
'use_alternative_architecture': True,
'verbose': 1,
'train_val_split': 0.97,
'nEpochs': 400,
'val_freq': 100,
'obj_function': obj_function
}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Distance")
compiledGurobiModel.compile_from_data(get_decision_vars, P_train, X_train, params=params)
evaluate(compiledGurobiModel, P_test, X_test)
GUI / AI-Interface for Gurobi Models
In many organizations, especially those with non-technical staff, it is essential to provide an intuitive interface for interacting with optimization models. Our AI-powered GUI enables users to easily select, start, interrupt, and review Gurobi models without writing any code. Using natural language, users can request modifications, adjustments, and even interpret the model's solutions. This no-code interface bridges the gap between complex optimization models and the end-users who rely on them for decision-making.
You can start the causara GUI using the following command:
python
>>> import causara
>>> causara.GUI()
You can also create a shortcut on the Desktop using the command:
python
>>> import causara
>>> causara.create_shortcut()
Below, we use the simple TSP model from the Quickstart section to illustrate how our system integrates with the GUI and AI interface.
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["distance"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["distance"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_Tutorial")
compiledGurobiModel.compile(decision_vars_func=get_decision_vars, gurobi_func=gurobi, c=causara.Demos.TSP_real_data.c)
Adding a README to the Model
Providing a README for your Gurobi model offers essential context and documentation, which is especially valuable when non-technical users interact with
the model via the AI interface. The README explains the meaning of the input data (p) and provides details about the decision variables.
In this demo, we describe the TSP problem, noting that p['cities'] is a binary vector where each entry indicates whether a city is
included in the route. Additionally, we list the city names for clarity. This additional context helps the AI interface understand the model better,
thereby facilitating more accurate natural language modifications and insightful solution presentations.
cities = ["Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol", "Newcastle upon Tyne", "Leicester", "Coventry",
"Bradford", "Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham", "Derby", "Southampton", "Portsmouth",
"Plymouth", "Exeter", "Norwich", "Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath", "Preston",
"Oxford", "Cambridge", "Carlisle"]
compiledGurobiModel.set_README(f"This is a classic Traveling Salesman Problem (TSP) model. The input p['cities'] is a binary vector of length 30,
where p['cities'][i] = 1 indicates that city i is to be included in the route. The model seeks a closed route (i.e., starting and ending at city 0)
that minimizes the total travel distance. The list of cities is as follows: {cities}.")
Now we can upload and save this model to the cloud, making it accessible via our GUI and AI-Interface.
compiledGurobiModel.upload()
Adding a Metric
A metric is a quantitative measure that summarizes a key aspect of your optimization model’s performance. In our context, a metric function extracts and formats information from the model's inputs and outputs, presenting the results in an easily understandable format. Metrics help users quickly grasp the quality and characteristics of a solution without having to interpret raw numerical data.
A metric function must take as inputs the three parameters (p, c, x) and return two lists
of equal size: one containing labels (a list of strings) and the other containing corresponding values. In our demo below,
the metric reconstructs the optimized route as a human-readable string by mapping the positions in the route back to city names.
This metric works as follows: It first determines which cities are selected based on the binary vector p["cities"].
Then, using the solution data in x["x"], it reconstructs the order in which these cities are visited. Finally,
it creates labels (e.g., "City 1", "City 2", etc.) and assigns the corresponding city names from a predefined list.
The result is a clear and concise description of the route.
def metric(p, c, x):
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Identify which cities are selected
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
labels = [f"City {i+1}" for i in range(n)]
values = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
return labels, values
compiledGurobiModel.add_metric("Route", metric, explanation="The optimized route as a human-readable string")
We can also create a metric using AI. With this feature, you simply provide a natural language description of what the metric should display. For example, you can request a metric that calculates the number of days required for a route if you drive a maximum of 8 hours per day and always sleep in one of the cities. The AI will then generate a metric that not only reports the total travel time divided by driving hours but also details for each day, including the city where you will sleep and the driving hours completed.
compiledGurobiModel.generate_AI_metric(user_request="Please generate a metric that prints how many days it takes for the route
if you drive max 8h per day and always sleep in one of the cities. Further tell me for each night in which city I will sleep and
after how many hours of driving during the day I arrive there. Note that I can drive 80km per hour. Example: if the route is
'City A' -> 'City B' -> ... -> 'City A', then the schedule could look something like: Day 1: 'City E' after <> hours.
Day 2: 'City J' after <> hours. ... 'City A' after <> hours.")
compiledGurobiModel.print_all_metric_names()
compiledGurobiModel.upload()
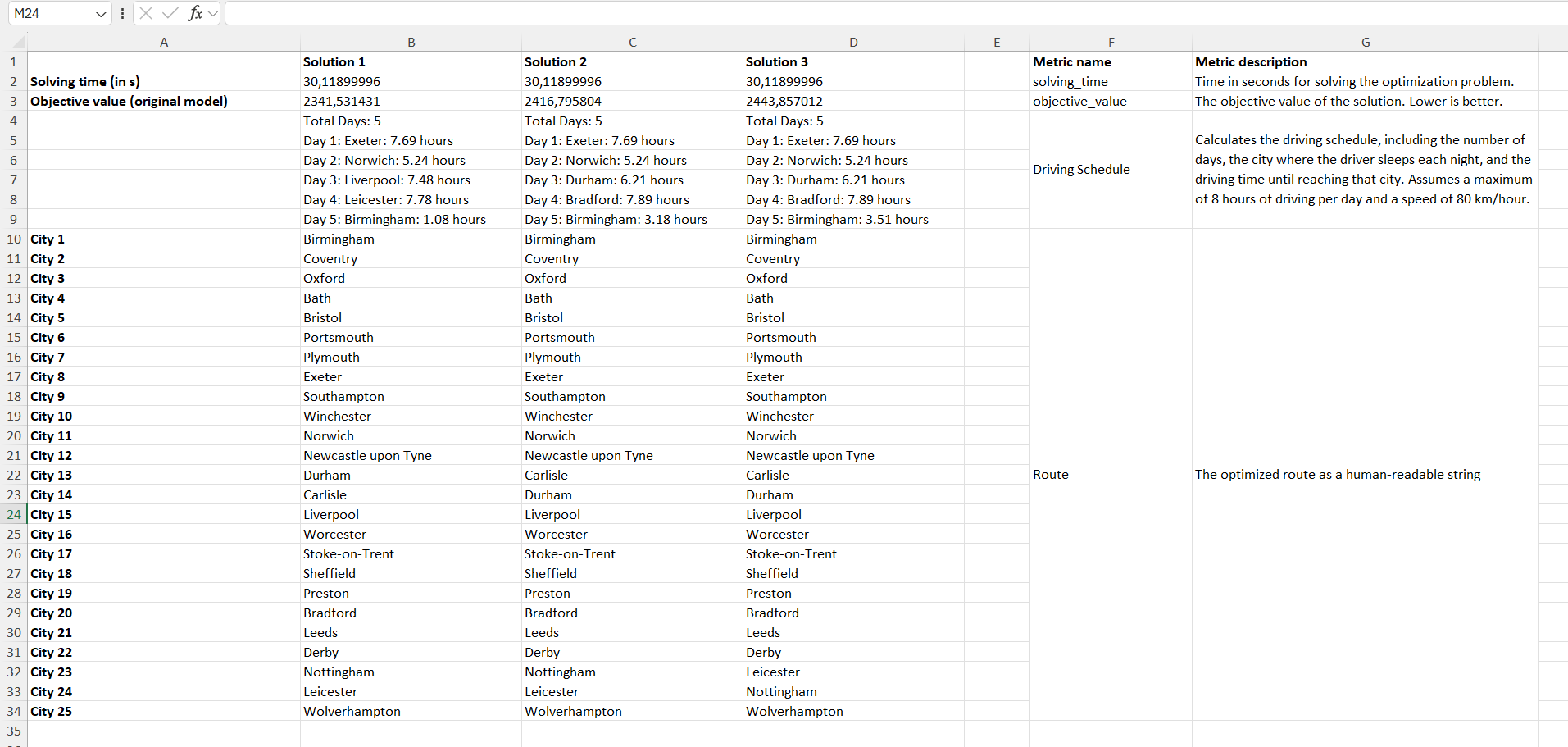
When you run this model in the GUI and click on "Summary," an Excel spreadsheet will open displaying the metrics for each solution.
In the screenshot, you can see the summary generated by the GUI. Our custom metric, named "Route", displays the optimized tour in a clear, human-readable format by showing which city is visited at each position along the route. In addition, the AI-generated metric "Driving Schedule" provides an estimated travel schedule: it calculates the number of days required to complete the tour under the constraints of driving at a maximum speed of 80 km/h and no more than 8 hours per day. This metric details, for each day, the city where you would stop for the night along with the total driving hours for that day.
Adding Scripts
You can enhance your model by adding four types of custom scripts. These scripts enable you to integrate external data, visualize results, export solutions, and compute real-world objective values.
-
read(): A custom Python function that retrieves a problem instance (p). For example, it may extract data from a SQL database or read it from a file. -
view(p, c, x): A function for representing or visualizing the solution in a user-friendly manner. -
write(p, c, x): A function that writes the solution back into other parts of your IT systems, such as storing it in a database or sending an email notification. -
objective(p, c, x): A function that computes and retrieves a real-world objective value for a given solutionx.
Below is a demonstration of how to integrate custom scripts into our TSP Gurobi model:
-
read(): This script retrieves a problem instance. In the demo, it randomly generates a binary vector indicating which cities are to be included in the route. -
view(p, c, x): This script visualizes the solution. It uses the Folium library to create a map that displays the route. The function reconstructs the route from the solution variables, retrieves the corresponding coordinates for each city, and then adds markers and a connecting polyline to the map. -
write(p, c, x): This script is designed for processing and storing the selected solution. In a real-world application, you might use it to write the solution back into a database or send notifications via email. -
objective(p, c, x): This script fetches the actual objective value from external IT systems. For demonstration purposes, it simply returns the value42.
After defining these scripts, they are added to the compiled Gurobi model. Finally, the model is uploaded to the cloud, making it accessible via the GUI.
def read():
# Create a random problem instance with 20 cities in the route
arr = np.array([1] * 20 + [0] * 10)
np.random.shuffle(arr)
p = {"cities": arr}
return p
def view(p, c, x):
import folium
import webbrowser
import os
from pathlib import Path
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Verified hard-coded coordinates (latitude, longitude)
city_coords = {
"Birmingham": (52.48142, -1.89983),
"Leeds": (53.79648, -1.54785),
"Sheffield": (53.38297, -1.46590),
"Manchester": (53.48095, -2.23743),
"Liverpool": (53.41058, -2.97794),
"Bristol": (51.45523, -2.59665),
"Newcastle upon Tyne": (54.97328, -1.61396),
"Leicester": (52.63860, -1.13169),
"Coventry": (52.40656, -1.51217),
"Bradford": (53.79391, -1.75206),
"Kingston upon Hull": (53.74460, -0.33525),
"Stoke-on-Trent": (53.00415, -2.18538),
"Wolverhampton": (52.58547, -2.12296),
"Nottingham": (52.95360, -1.15047),
"Derby": (52.92277, -1.47663),
"Southampton": (50.90395, -1.40428),
"Portsmouth": (50.79899, -1.09125),
"Plymouth": (50.37153, -4.14305),
"Exeter": (50.72360, -3.52751),
"Norwich": (52.62783, 1.29834),
"Chester": (53.19050, -2.89189),
"Durham": (54.77676, -1.57566),
"Winchester": (51.06513, -1.31870),
"Gloucester": (51.86568, -2.24310),
"Worcester": (52.18935, -2.22001),
"Bath": (51.37510, -2.36172),
"Preston": (53.76282, -2.70452),
"Oxford": (51.75222, -1.25596),
"Cambridge": (52.20000, 0.11667),
"Carlisle": (54.89510, -2.93820)
}
# Identify which cities are selected based on p["cities"]
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
# Build the route using the selected cities and their order
route = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
route.append(route[0]) # Complete the circuit by returning to the start
# Retrieve coordinates from the hard-coded dictionary
coordinates = []
for city in route:
if city in city_coords:
coordinates.append(city_coords[city])
else:
print(f"Could not find coordinates for {city}")
if not coordinates:
print("No coordinates found. Exiting.")
return
# Create a folium map centered on the first city
m = folium.Map(location=coordinates[0], zoom_start=6)
# Add markers for each city along the route
for i, (lat, lon) in enumerate(coordinates):
folium.Marker([lat, lon], popup=route[i]).add_to(m)
# Draw a polyline connecting the cities in the order of the route
folium.PolyLine(locations=coordinates, color="blue", weight=2.5, opacity=1).add_to(m)
file_name = "map.html"
documents_folder = Path.home() / "Documents"
documents_folder.mkdir(parents=True, exist_ok=True)
html_file = documents_folder / file_name
print(html_file)
m.save(html_file)
# Convert the relative path to an absolute file URL
file_path = os.path.abspath(html_file)
file_url = "file://" + file_path
webbrowser.open(file_url)
def write(p, c, x):
print("Processing and storing the chosen solution x with your own code.")
def objective(p, c, x):
print("Retrieving the actual objective value from external IT sources.")
return 42 # For demonstration purposes, returns 42
compiledGurobiModel.add_read_script(read)
compiledGurobiModel.add_view_script(view)
compiledGurobiModel.add_write_script(write)
compiledGurobiModel.add_objective_script(objective)
compiledGurobiModel.upload()
Video Tutorial
This is the complete code from all four previous sections including a README, a custom metric, an AI-generated metric and scripts for read,
view, write and objective. The video tutorial below uses the model created with this code.
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
import numpy as np
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["distance"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["distance"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
def metric(p, c, x):
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Identify which cities are selected
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
labels = [f"City {i+1}" for i in range(n)]
values = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
return labels, values
def read():
# Create a random problem instance with 25 cities in the route
arr = np.array([1] * 20 + [0] * 10)
np.random.shuffle(arr)
p = {"cities": arr}
return p
def view(p, c, x):
import folium
import webbrowser
import os
from pathlib import Path
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Verified hard-coded coordinates (latitude, longitude)
city_coords = {
"Birmingham": (52.48142, -1.89983),
"Leeds": (53.79648, -1.54785),
"Sheffield": (53.38297, -1.46590),
"Manchester": (53.48095, -2.23743),
"Liverpool": (53.41058, -2.97794),
"Bristol": (51.45523, -2.59665),
"Newcastle upon Tyne": (54.97328, -1.61396),
"Leicester": (52.63860, -1.13169),
"Coventry": (52.40656, -1.51217),
"Bradford": (53.79391, -1.75206),
"Kingston upon Hull": (53.74460, -0.33525),
"Stoke-on-Trent": (53.00415, -2.18538),
"Wolverhampton": (52.58547, -2.12296),
"Nottingham": (52.95360, -1.15047),
"Derby": (52.92277, -1.47663),
"Southampton": (50.90395, -1.40428),
"Portsmouth": (50.79899, -1.09125),
"Plymouth": (50.37153, -4.14305),
"Exeter": (50.72360, -3.52751),
"Norwich": (52.62783, 1.29834),
"Chester": (53.19050, -2.89189),
"Durham": (54.77676, -1.57566),
"Winchester": (51.06513, -1.31870),
"Gloucester": (51.86568, -2.24310),
"Worcester": (52.18935, -2.22001),
"Bath": (51.37510, -2.36172),
"Preston": (53.76282, -2.70452),
"Oxford": (51.75222, -1.25596),
"Cambridge": (52.20000, 0.11667),
"Carlisle": (54.89510, -2.93820)
}
# Identify which cities are selected based on p["cities"]
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
# Build the route using the selected cities and their order
route = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
route.append(route[0]) # Complete the circuit by returning to the start
# Retrieve coordinates from the hard-coded dictionary
coordinates = []
for city in route:
if city in city_coords:
coordinates.append(city_coords[city])
else:
print(f"Could not find coordinates for {city}")
if not coordinates:
print("No coordinates found. Exiting.")
return
# Create a folium map centered on the first city
m = folium.Map(location=coordinates[0], zoom_start=6)
# Add markers for each city along the route
for i, (lat, lon) in enumerate(coordinates):
folium.Marker([lat, lon], popup=route[i]).add_to(m)
# Draw a polyline connecting the cities in the order of the route
folium.PolyLine(locations=coordinates, color="blue", weight=2.5, opacity=1).add_to(m)
file_name = "map.html"
documents_folder = Path.home() / "Documents"
documents_folder.mkdir(parents=True, exist_ok=True)
html_file = documents_folder / file_name
print(html_file)
m.save(html_file)
# Convert the relative path to an absolute file URL
file_path = os.path.abspath(html_file)
file_url = "file://" + file_path
webbrowser.open(file_url)
def write(p, c, x):
print("Processing and storing the chosen solution x with your own code.")
def objective(p, c, x):
print("Retrieving the actual objective value from external IT sources.")
return 42 # For demonstration purposes, returns 42
def get_decision_vars(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
decision_vars = DecisionVars()
decision_vars.add_binary_vars("x", (n, n))
return decision_vars
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_Tutorial")
compiledGurobiModel.compile(decision_vars_func=get_decision_vars, gurobi_func=gurobi, c=causara.Demos.TSP_real_data.c)
compiledGurobiModel.set_time_limit(time_limit=30)
cities = ["Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol", "Newcastle upon Tyne", "Leicester", "Coventry",
"Bradford", "Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham", "Derby", "Southampton", "Portsmouth",
"Plymouth", "Exeter", "Norwich", "Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath", "Preston",
"Oxford", "Cambridge", "Carlisle"]
compiledGurobiModel.set_README(f"This is a classic TSP problem. p['cities'] is a binary vector of length 30 where p['cities'][i] = 1 indicates that city i should be part of the route. "
f"The cities are: {cities}. The route must be closed, so always consider the time going from the last city back to the first city.")
compiledGurobiModel.generate_AI_metric(user_request="Please generate a metric that prints how many days it takes for the route if you drive max 8h per day and always sleep in "
"one of the cities. Further tell me for each night in which city I will sleep and after how many hours of driving during the "
"day I arrive there. Note that I can drive 80km per hour. Example: if the route is 'City A' -> 'City B' -> ... -> "
"'City A', then the schedule could look something like: Day 1: 'City E' after <> hours. Day 2: 'City J' after <> hours. ... 'City A' "
"after <> hours.")
compiledGurobiModel.add_metric("Route", metric, explanation="The optimized route as a human-readable string")
compiledGurobiModel.print_all_metric_names()
compiledGurobiModel.add_read_script(read)
compiledGurobiModel.add_view_script(view)
compiledGurobiModel.add_write_script(write)
compiledGurobiModel.add_objective_script(objective)
compiledGurobiModel.upload()
You can start the causara GUI using the following command:
python
>>> import causara
>>> causara.GUI()
You can also create a shortcut on the Desktop using the command:
python
>>> import causara
>>> causara.create_shortcut()
Managing Your Account
This section provides comprehensive instructions on how to manage your account on our platform. You can upload, download, and delete models or datasets,
and view detailed information about your account and stored models using the printInfos() function. These tools ensure that you have full control over
your optimization models and data.
For example, once you compile a model using compile(), you can upload it to the cloud to securely store it and make it accessible from anywhere.
Similarly, you can upload any real-world data associated with your model for later fine-tuning or evaluation.
from causara import *
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP")
compiledGurobiModel.compile(...)
compiledGurobiModel.upload()
The code above compiles your TSP model and then uploads it to our cloud service. Once uploaded, you can also manage associated real-world data.
real_world_data = Real_World_Data()
for i in range(3):
data = compiledGurobiModel.solve(P.iloc[i])
real_world_data.append(data)
real_world_data.upload("your_key", "TSP")
To check your account details and view the status of your uploaded models or datasets, use the printInfos() function.
This function prints important metadata such as available models / datasets, API usage and remaining tokens.
printInfos(key="your_key")
If you need to retrieve your stored model or dataset, you can download it from the cloud. This functionality allows you to restore or further process your data locally.
real_world_data = Real_World_Data()
real_world_data.download("your_key", "TSP")
print(real_world_data)
Finally, when a model or dataset is no longer required, you can permanently remove it from the cloud using the deleteModel() and deleteDataset() functions.
deleteModel(key="your_key", name="TSP")
deleteDataset(key="your_key", name="TSP")
printInfos(key="your_key")