Get Started
What is Mathematical Optimization?
Mathematical optimization is the process of finding the best solution to a problem defined by an objective function and constraints. A common example is maximizing profits in a factory’s production schedule or minimizing travel distances in a delivery network. It translates real-world scenarios into mathematical models that seek maximum or minimum values. Constraints encapsulate practical or theoretical limitations, guiding the feasible solution space.
What is Gurobi?
Gurobi (www.gurobi.com) is a leading solver for advanced mathematical optimization problems. It leverages efficient algorithms and parallel computing to handle large-scale models at high speed. Widely adopted across industries, Gurobi empowers organizations to make data-driven decisions and achieve cost savings.
What is Causara?
Causara is a Python package with a user-friendly graphical interface that simplifies creating, modifying, and interacting with Gurobi models. It allows you to generate models directly from your data—even without a predefined objective function—by translating your information into a Gurobi model. You can also build models using pure Python code and make adjustments with simple natural language commands through the GUI, among many other advanced features.
Installation
Start by installing the Causara package via pip
pip install causaraNext, generate a test key. You will receive it via email:
python
>>> import causara
>>> causara.get_test_key("my_mail@xxx")
Quickstart
This guide demonstrates how to use Causara to compile and solve an optimization problem. In this example, we tackle the Traveling Salesman Problem (TSP) using Gurobi. Our objective is to determine the optimal route that minimizes the total travel distance among a selected group of cities.
Remember, any optimization problem can be expressed as:
x* = argmax f(p, c, x)
where:
- p represents the problem variables (inputs).
- c represents the constant data (fixed parameters).
- x represents the decision variables.
Overview of the Demo:
The main class in Causara is CompiledGurobiModel. This class integrates a base Gurobi model and allows you to add post-processing functions, fine-tune the model, and more.
You can add a base Gurobi model to your CompiledGurobiModel object using one of these three methods:
compile_from_gurobi()compile_from_data()compile_from_python()
In this quickstart, we demonstrate the compile_from_gurobi() method. With this method, you provide a function that returns a gurobipy.Model object, built using the specified problem parameters (p) and constants (c).
Key Classes and Variables in Causara:
p(problem variables): A dictionary with keys as strings and values as int, float, or numpy array.c(constants): A dictionary containing fixed data required by the model.x(decision variables): A dictionary that holds the variables whose values are determined by the optimization.CompiledGurobiModel: The primary class for working with optimization models in Causara.Real_World_Data: A class for storing real-world data, including the problem parameters p and their corresponding optimal solution x* for future fine-tuning (not used in this quickstart).
TSP Model Function:
The function below defines the TSP model using Gurobi. It sets up the optimization problem by:
- Creating binary decision variables for the route.
- Adding constraints to ensure each selected city is assigned a unique position in the route.
- Ensuring that the tour starts (and eventually ends) at city 0.
- Defining an objective function that minimizes the total travel distance.
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
import numpy as np
def tsp(p, c):
# Identify selected cities based on p["cities"]
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
# Create a new Gurobi model
model = gp.Model()
# Create binary variables: route[i, j] == 1 indicates that selected city i is assigned to position j in the route.
route = model.addVars(n, n, vtype=GRB.BINARY, name='route')
# Add constraints: each city must be assigned to one unique position, and each position must be filled by one city.
for i in range(n):
model.addConstr(gp.quicksum(route[i, j] for j in range(n)) == 1)
model.addConstr(gp.quicksum(route[j, i] for j in range(n)) == 1)
# Ensure that city 0 starts the route.
model.addConstr(route[0, 0] == 1)
# Define the objective function to minimize the total route length.
route_length = 0
for city1 in range(n):
c1 = selected_cities[city1]
for pos1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for pos2 in range(n):
if pos2 == pos1 + 1:
route_length += c["distance"][c1][c2] * route[city1, pos1] * route[city2, pos2]
if pos1 == 0 and pos2 == n - 1:
route_length += c["distance"][c1][c2] * route[city1, pos2] * route[city2, pos1]
model.setObjective(route_length, GRB.MINIMIZE)
return model
Running the Model with Causara:
The code below shows how to compile and solve the TSP model using Causara. The process includes:
- Creating a CompiledGurobiModel object with your credentials.
- Compiling the base Gurobi model and specifying the target variables.
- Solving the model for a random problem instance.
- Displaying the results.
- NOTE: You must insert your own key, otherwise it will throw an error
# Create a compiled model object with your unique key and model name.
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP")
# Compile the TSP model, specifying 'route' as the target variable.
compiledGurobiModel.compile_from_gurobi(tsp, target_vars=["route"], c=causara.Demos.TSP_real_data.c)
# Create a random problem instance
p = {"cities": np.random.choice([0, 1], size=30)}
# Solve the compiled model and select the first solution
x, x_complete, obj_value = compiledGurobiModel.solve(p)[0]
# Display the results.
print(f"x: {x}")
print(f"objective value: {obj_value}")
Understanding the Output:
The solve() method returns a list of tuples in the format (x, x_complete, obj_value).
The number of tuples in the list is determined by the num_solutions parameter of the solve() method.
If Gurobi finds that many solutions, the list will contain exactly that many tuples.
x: Contains the solution for the variables specified in target_vars (in this case, theroute).x_complete: Contains all solution variables, including auxiliary ones. This comprehensive output is useful for further analysis and debugging.obj_value: This is a float representing the objective value of this solution.
Complete Demo Code:
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
import numpy as np
def tsp(p, c):
# Identify selected cities based on p["cities"]
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
# Create a new Gurobi model
model = gp.Model()
# Create binary variables: route[i, j] == 1 indicates that selected city i is assigned to position j in the route.
route = model.addVars(n, n, vtype=GRB.BINARY, name='route')
# Add constraints: each city must be assigned to one unique position, and each position must be filled by one city.
for i in range(n):
model.addConstr(gp.quicksum(route[i, j] for j in range(n)) == 1)
model.addConstr(gp.quicksum(route[j, i] for j in range(n)) == 1)
# Ensure that city 0 starts the route.
model.addConstr(route[0, 0] == 1)
# Define the objective function to minimize the total route length.
route_length = 0
for city1 in range(n):
c1 = selected_cities[city1]
for pos1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for pos2 in range(n):
if pos2 == pos1 + 1:
route_length += c["distance"][c1][c2] * route[city1, pos1] * route[city2, pos2]
if pos1 == 0 and pos2 == n - 1:
route_length += c["distance"][c1][c2] * route[city1, pos2] * route[city2, pos1]
model.setObjective(route_length, GRB.MINIMIZE)
return model
# Create a compiled model object with your unique key and model name.
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP")
# Compile the TSP model, specifying 'route' as the target variable.
compiledGurobiModel.compile_from_gurobi(tsp, target_vars=["route"], c=causara.Demos.TSP_real_data.c)
# Create a random problem instance
p = {"cities": np.random.choice([0, 1], size=30)}
# Solve the compiled model and select the first solution
x, x_complete, obj_value = compiledGurobiModel.solve(p)[0]
# Display the results.
print(f"x: {x}")
print(f"objective value: {obj_value}")
Learn a Gurobi Model from Data
As introduced in the Quickstart section, every optimization problem can be formulated as:
x* = argmax f(p, c, x)
where:
- p represents the problem variables (inputs).
- c represents the constant data (fixed parameters).
- x represents the decision variables.
We now want to learn this function f that encodes this optimization problem given a set of training data [(p,x*)].
We therefore don't need to know how to encode an optimization problem with Gurobi.
compile_from_data(P, X, P_val, X_val, params)
P: A pandas DataFrame or a list of dictsX: A pandas DataFrame or a list of dictsP_val(optional): Validation input data. A pandas DataFrame or a list of dictsX_val(optional): Validation output data. A pandas DataFrame or a list of dictsparams: A dictionary of hyperparameters that configure the neural network
In the following we will present two demos on how to use this feature.
Predicting Molecules with a Specified Property Vector
In this section, we demonstrate how to learn a Gurobi model which can predict a molecule that has a specified property vector.
We use the QM9 dataset, a collection of small organic molecules from quantum chemistry simulations, to illustrate this process.
QM9 provides computed molecular properties, such as dipole moments or polarizabilities, making it well-suited for tasks like ours.
In the mathematical framework x* = argmax f(p, c, x); p is the property vector (8 dimensions),
c is empty, x is the molecule and f is the Gurobi model we want to learn.
1. Reading and Preparing the Dataset
We use the QM9 dataset, which is distributed as a compressed file named dsgdb9nsd.xyz.tar.bz2. A direct download link is available from https://figshare.com/ndownloader/files/3195389. You can also use this command to download the dataset:
wget --no-check-certificate -O dsgdb9nsd.xyz.tar.bz2 "https://figshare.com/ndownloader/files/3195389"This dataset contains:
- properties: For each molecule, we have a vector of numerical values describing different physical/chemical properties (e.g., dipole moment, HOMO-LUMO gap).
- molecules: Molecules are represented in SMILES notation. For learning a Gurobi model we need
xto be a binary vector. We could directly represent the molecule as a graph, but we decided to use binary fingerprints in this demo since it is more compact. We used the MACCS fingerprints
from rdkit import RDLogger
RDLogger.DisableLog('rdApp.*')
import numpy as np
from causara import *
import matplotlib.pyplot as plt
from causara.Demos.MoleculePrediction import read_dsg_dataset
dataset_file = "/path/to/dsgdb9nsd.xyz.tar.bz2"
properties, fingerprints = read_dsg_dataset(dataset_file)
print(f"\nproperties.shape: {properties.shape}")
print(f"fingerprints.shape: {fingerprints.shape}\n")

2. Visualizing the Data
We can now plot the distribution of each molecular property.
def plot_data(properties, fingerprints):
import matplotlib
matplotlib.use("TkAgg")
# Plot distribution for every feature in normalized_properties
num_features = properties.shape[1]
fig, axes = plt.subplots(4, 2, figsize=(16, 12)) # Create a 4x2 grid
axes = axes.flatten() # Flatten the 2D array of axes to 1D for easier iteration
labels = [
"Dipole moment",
"Isotropic polarizability",
"Energy of Highest occupied molecular orbital (HOMO)",
"Energy of Lowest occupied molecular orbital (LUMO)",
"Gap, difference between LUMO and HOMO",
"Electronic spatial extent",
"Zero point vibrational energy",
"Internal energy at 0 K"
]
for i in range(num_features):
axes[i].hist(properties[:, i], bins=100, color='skyblue', edgecolor='black', alpha=0.7)
axes[i].set_title(labels[i])
axes[i].set_xlabel('Normalized Value')
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
matplotlib.use("Agg")
plot_data(properties, fingerprints)
3. Splitting the Dataset into Training and Test Subsets
After loading the dataset, we partition it into two parts:
- properties_train, fingerprints_train: Used to train or compile the Gurobi model.
- properties_test, fingerprints_test: Used to evaluate the model's performance by comparing predictions against real molecular data.
properties_train = properties[:40000]
fingerprints_train = fingerprints[:40000]
properties_test = properties[40000:]
fingerprints_test = fingerprints[40000:]
4. Compiling the Model from Data
We call compile_from_data() on our CompiledGurobiModel object to create a Gurobi model f(p,x)
such that for every (p,x) pair it holds that the molecule x is the optimal solution when faced with the property vector p:
params = {
'nHiddens': [128, 128, 128, 256],
'batchSize': 500,
'lr': 0.0013,
'solving_time': 0.5,
'train_val_split': 0.998,
'nEpochs': 100,
'val_freq': 50,
'intraBatchOptimization': False,
'buffer': 0.01
}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Molecule")
compiledGurobiModel.compile_from_data(
P={"properties": properties_train},
X={"fingerprints": fingerprints_train},
params=params)
5. Evaluating the Model
Once compiled, we use the evaluate() function to test the model on unseen data. The process is:
- Randomly choose a
target_propertyvector fromproperties_test. - Compute the objective value for all molecules in the test set to see how well each candidate matches the target property.
- Identify the top candidates and measure how close their properties are to the target (using an absolute distance metric).
- Report the best match among these top candidates and provide its rank if we sorted all molecules by their distance to the target.
Complete Code
Below is the entire code, putting together all of the above steps. Adjust the dataset_file path according to where you have placed
dsgdb9nsd.xyz.tar.bz2 and insert your TEST-key.
from rdkit import RDLogger
RDLogger.DisableLog('rdApp.*')
import numpy as np
from causara import *
import matplotlib.pyplot as plt
from causara.Demos.MoleculePrediction import read_dsg_dataset
def plot_data(properties, fingerprints):
import matplotlib
matplotlib.use("TkAgg")
# Plot distribution for every feature in normalized_properties
num_features = properties.shape[1]
fig, axes = plt.subplots(4, 2, figsize=(16, 12)) # Create a 4x2 grid
axes = axes.flatten() # Flatten the 2D array of axes to 1D for easier iteration
labels = [
"Dipole moment",
"Isotropic polarizability",
"Energy of Highest occupied molecular orbital (HOMO)",
"Energy of Lowest occupied molecular orbital (LUMO)",
"Gap, difference between LUMO and HOMO",
"Electronic spatial extent",
"Zero point vibrational energy",
"Internal energy at 0 K"
]
for i in range(num_features):
axes[i].hist(properties[:, i], bins=100, color='skyblue', edgecolor='black', alpha=0.7)
axes[i].set_title(labels[i])
axes[i].set_xlabel('Normalized Value')
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
matplotlib.use("Agg")
def evaluate(compiledGurobiModel, properties_test, fingerprints_test, num_tests=10):
"""
Evaluates the model's performance by:
1. Selecting a random target property vector
2. Retrieving objective values for all test molecules
3. Identifying top molecules according to the objective
4. Computing the absolute distance in property space
5. Determining the best match and its overall rank
"""
print("\n" + "=" * 50 + "\n" + "=" * 50 + "\n")
print("Evaluation Phase")
print("\n" + "=" * 50 + "\n" + "=" * 50 + "\n")
print(f"Number of candidate molecules: {len(properties_test)}\n")
for test in range(num_tests):
# 1. Select a random target property vector
target_property = properties_test[np.random.choice(len(properties_test))]
# 2. Retrieve objective values for all test molecules
obj_values = compiledGurobiModel.get_obj_values({"properties": target_property}, {"fingerprints": fingerprints_test})
# 3. Identify the top 10 candidates (largest objective values)
top10_indices = np.argsort(obj_values)[::-1][:10]
# 4. Compute absolute property distance for these top 10 candidates
top10_abs_dists = []
for i in range(10):
idx = top10_indices[i]
dist = np.sum(np.abs(properties_test[idx] - target_property))
top10_abs_dists.append(dist)
best_among_top10_idx = top10_indices[np.argmin(top10_abs_dists)]
best_abs_distance = np.min(top10_abs_dists)
# Calculate absolute distances for all molecules to find the rank of the best candidate
abs_dists = np.sum(np.abs(properties_test - target_property), axis=1)
sorted_indices = np.argsort(abs_dists) # ascending order
best_rank = np.where(sorted_indices == best_among_top10_idx)[0][0] + 1
# 5. Output results
print(f"Test {test + 1}")
print("Target molecule property: ", [float(f"{value:.3f}") for value in target_property])
print("Property of predicted molecule: ", [float(f"{value:.3f}") for value in properties_test[best_among_top10_idx]])
print(f"Absolute distance between target property and predicted molecule: {best_abs_distance:.3f}")
print(f"Rank in absolute-distance ordering: {best_rank} out of {len(abs_dists)}")
print("\n" + "-" * 50 + "\n")
# Download the QM9 dataset from the link below and place it on your system
dataset_file = "/path/to/dsgdb9nsd.xyz.tar.bz2"
properties, fingerprints = read_dsg_dataset(dataset_file)
print(f"\nproperties.shape: {properties.shape}")
print(f"fingerprints.shape: {fingerprints.shape}\n")
# Visualize the data
plot_data(properties, fingerprints)
properties_train = properties[:40000]
fingerprints_train = fingerprints[:40000]
properties_test = properties[40000:]
fingerprints_test = fingerprints[40000:]
params = {
'nHiddens': [128, 128, 128, 256],
'batchSize': 500,
'lr': 0.0013,
'solving_time': 0.5,
'train_val_split': 0.998,
'nEpochs': 100,
'val_freq': 50,
'intraBatchOptimization': False,
'buffer': 0.01
}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Molecule")
compiledGurobiModel.compile_from_data(
P={"properties": properties_train},
X={"fingerprints": fingerprints_train},
params=params)
evaluate(compiledGurobiModel, properties_test, fingerprints_test)
Predicting a Graph with a Specified Distance Matrix
Let G = (V, E) be a graph, where V is the set of vertices and E is the set of edges. Given any graph, it is straightforward to compute the shortest path distance between every pair of vertices; the result is a distance matrix D.
However, the inverse problem—predicting a graph that corresponds to a specified distance matrix—is highly challenging. This is because the problem is inherently a bilevel optimization problem. At the upper level, we seek a graph whose induced distance matrix closely matches the target distance matrix. At the lower level, the graph must satisfy combinatorial constraints (e.g., connectivity, edge existence), and the distances are computed based on the graph structure. These two levels are interdependent, making the overall problem difficult to solve directly.
We want to learn a Gurobi model that predicts a graph for a specified distance matrix:
In this demo, we leverage the fact that computing the distance matrix from a given graph is relatively simple. We generate large amounts of synthetic training data by creating random graphs and computing their corresponding distance matrices. The objective is to train a model that, when presented with a target distance matrix (p), outputs a graph (x) that satisfies the desired distance constraints.
from causara import *
from causara.Demos.DistanceMatrix import generate_data, get_distance_matrix, get_adj_matrix
print("Creating synthetic training data")
P_train, X_train = generate_data(n=7000, size=20)
P_test, X_test = generate_data(n=50, size=20)
We then define an objective function. Note: this objective function is used only for validation. It returns 0 if the predicted graph is correct (i.e. the computed distance matrix for the predicted graph exactly matches the specified distance matrix) and 1 otherwise.
def obj_function(p, x, x_pred):
adj_matrix = get_adj_matrix(x_pred["X"])
distance_matrix_pred = get_distance_matrix(adj_matrix)
if p["P"].shape == distance_matrix_pred.shape and equal(p["P"], distance_matrix_pred):
return 0
else:
return 1
Finally, we train the Gurobi model using the method compile_from_data().
Complete Code
from causara import *
from causara.Demos.DistanceMatrix import generate_data, get_distance_matrix, get_adj_matrix
def evaluate(compiledGurobiModel, P_test, X_test):
numCorrect = 0
for i in range(len(P_test)):
p = P_test.iloc[i]
x = X_test.iloc[i]
x_predicted, _, obj_value = compiledGurobiModel.solve(p, gurobi_params={"TimeLimit": 0.5}, useInternalSolver=True)[0]
if equal(x_predicted["X"], x["X"]):
numCorrect += 1
print(f"Result: {numCorrect} / {len(P_test)} correct")
def obj_function(p, x, x_pred):
adj_matrix = get_adj_matrix(x_pred["X"])
distance_matrix_pred = get_distance_matrix(adj_matrix)
if p["P"].shape == distance_matrix_pred.shape and equal(p["P"], distance_matrix_pred):
return 0
else:
return 1
print("Creating synthetic training data")
P_train, X_train = generate_data(n=7000, size=20)
P_test, X_test = generate_data(n=50, size=20)
params = {
'num_reasoning_cycles': 2,
'nHiddens': [256, 256, 512],
'batchSize': 500,
'lr': 0.0013,
'output_type': 'binary',
'solving_time': 0.1,
'use_alternative_architecture': True,
'verbose': 1,
'train_val_split': 0.97,
'nEpochs': 400,
'val_freq': 100,
'obj_function': obj_function
}
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Distance")
compiledGurobiModel.compile_from_data(P_train, X_train, params=params)
evaluate(compiledGurobiModel, P_test, X_test)
Compile Plain Python Code into a Gurobi Model
While it is usually straightforward to define an objective function and constraints in plain Python, translating this logic into a Gurobi model can be complex and error-prone. Our approach leverages large language models (LLMs) to automatically convert plain Python code into a fully functional Gurobi model. This simplifies the model development process, allowing you to focus on the core logic of your optimization problem without getting bogged down by the intricacies of Gurobi's API.
compile_from_python(func, sense, P_val, target_vars, forceNewCompiling, num_trials)
func: A Python function that defines your optimization problem. This function should include your objective and constraints expressed in plain Python and must have three parameters(p,c,x)all of whom are dicts.sense: Specifies the optimization sense. It must be one ofGRB.MAXIMIZEorGRB.MINIMIZEP_val: A pandas DataFrame containing validation input data. The data inP_valis used to verify that the compiled model correctly captures the intended logic of your function.target_varsA list of strings indicating the names of the decision variables in your Gurobi model. If not provided, the method attempts to automatically infer these names from the source code offunc.c: A dictionary containing constant parameters required by your model. This can include fixed data or precomputed matrices that are used in your optimization.forceNewCompiling: A boolean flag. If set toTrue, the method will force a new compilation of the model even if a previously compiled version exists.num_trials: An integer indicating how many compilation trials to perform. Multiple trials may be used to ensure the best translation of your Python code into the Gurobi model.
In the following we will present two demos on how to use this feature
n-agent TSP
The n-agent Traveling Salesman Problem (TSP) extends the classic TSP to multiple agents. In this formulation, n agents are assigned routes so that every city is visited by at least one agent. All agents start and end their routes at the same designated city (commonly city 0). The goal is to minimize the maximum route length (or travel time) among all agents, ensuring that no single agent is overburdened and that the overall completion time is optimized.
We can easily encode this logic into a simple Python function n_agent_TSP(p, c, x) using Python syntax like
in, assert, max, and more. Note: the Python function must always return a scalar value (the objective value).
For creating decision variables use Var(shape, type, x, name, lowerBound, upperBound). It will return a numpy array of that shape.
def n_agent_TSP(p, c, x):
# Extract parameters from the problem instance.
distances = p["distances"]
num_cities = p["num_cities"]
num_agents = p["num_agents"]
# Define the maximum route length (each route covers all cities).
max_route_length = num_cities
# Define the decision variable 'routes' as a 2D variable
routes = Var((max_route_length, num_agents), Types.INTEGER, x, "routes", lowerBound=0, upperBound=num_cities-1)
# Ensure that all agents start and end at city 0.
assert equal(routes[0], 0) # All agents start at city 0.
assert equal(routes[num_cities-1], 0) # All agents end at city 0.
# Ensure that every city is visited by at least one agent.
for city_nr in range(num_cities):
assert city_nr in routes
# Calculate the total distance traveled by each agent.
paths = [0] * num_agents
for agent_nr in range(num_agents):
for position_nr in range(num_cities-1):
city_nr = routes[position_nr][agent_nr]
next_city_nr = routes[position_nr + 1][agent_nr]
paths[agent_nr] += distances[city_nr][next_city_nr]
# The objective is to minimize the maximum distance traveled among all agents.
cost = max(paths)
return cost
Next, we generate random problem instances for validating the compiled Gurobi model and compile the model using compile_from_python().
P_val = causara.Demos.n_agent_TSP.generate_P(3, num_cities=15, num_agents=3)
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="n_agent_TSP")
compiledGurobiModel.compile_from_python(func=n_agent_TSP, sense=GRB.MINIMIZE, P_val=P_val, target_vars=["routes"], forceNewCompiling=True)
Finally, we test our compiled model by solving one of the generated problem instances and printing the resulting routes for each agent.
Complete Code
from causara import *
import causara
from gurobipy import GRB
def n_agent_TSP(p, c, x):
# Extract parameters from the problem instance.
distances = p["distances"]
num_cities = p["num_cities"]
num_agents = p["num_agents"]
# Define the maximum route length (each route covers all cities).
max_route_length = num_cities
# Define the decision variable 'routes' as a 2D variable
routes = Var((max_route_length, num_agents), Types.INTEGER, x, "routes", lowerBound=0, upperBound=num_cities-1)
# Ensure that all agents start and end at city 0.
assert equal(routes[0], 0) # All agents start at city 0.
assert equal(routes[num_cities-1], 0) # All agents end at city 0.
# Ensure that every city is visited by at least one agent.
for city_nr in range(num_cities):
assert city_nr in routes
# Calculate the total distance traveled by each agent.
paths = [0] * num_agents
for agent_nr in range(num_agents):
for position_nr in range(num_cities-1):
city_nr = routes[position_nr][agent_nr]
next_city_nr = routes[position_nr + 1][agent_nr]
paths[agent_nr] += distances[city_nr][next_city_nr]
# The objective is to minimize the maximum distance traveled among all agents.
cost = max(paths)
return cost
# Generate a random problem instance for n-agent TSP.
P_val = causara.Demos.n_agent_TSP.generate_P(3, num_cities=15, num_agents=3)
# Compile the Python function into a Gurobi model.
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="n_agent_TSP")
compiledGurobiModel.compile_from_python(func=n_agent_TSP, sense=GRB.MINIMIZE, P_val=P_val, target_vars=["routes"], forceNewCompiling=True)
# Select a problem instance and solve the model.
p = P_val.iloc[0]
x, _, obj_value = compiledGurobiModel.solve(p)[0]
print(f"\nObjective value: {obj_value}\n")
for agent_nr in range(p["num_agents"]):
route = x["routes"][:, agent_nr]
print(f"Route of agent {agent_nr}: {route}")
TSP with Time Windows
The Traveling Salesman Problem with Time Windows is a variant of the classic TSP where some cities must be visited within a specific time window. If the agent arrives too early or too late, the visit is considered invalid. This model is often used in scenarios like package delivery or service routing, where locations have strict availability periods.
It is straightforward to encode this problem in a plain Python function TSP_with_time_windows(p, c, x) that encodes these time window constraints.
The route must include all cities exactly once. For this constraint you can use the special constraint allDifferent(). If the agent
arrives at a city before or after its allowable interval, an assertion error is thrown, indicating an infeasible route. Note that error() is equivalent to assert False.
The objective is to minimize the total completion time of the route, starting at 8:00.
def TSP_with_time_windows(p, c, x):
distances = p["distances"]
num_cities = p["num_cities"]
time_window_start = p["time_window_start"]
time_window_end = p["time_window_end"]
# Define the route as a decision variable that assigns a city to each position.
route = Var(num_cities, Types.INTEGER, x, "route", lowerBound=0, upperBound=num_cities-1)
# Start the route at 8:00.
current_time = 8
# Ensure all cities are visited exactly once.
assert allDifferent(route)
# Traverse all cities in the order defined by 'route'.
for i in range(num_cities):
# If we haven't reached the last city, move to the next; otherwise, wrap around to the first city.
if i < num_cities - 1:
current_city = route[i]
next_city = route[i + 1]
else:
current_city = route[i]
next_city = route[0]
# If the current city has a time window, check feasibility.
if time_window_start[current_city] != -1:
if current_time < time_window_start[current_city] or current_time > time_window_end[current_city]:
error()
# Update the current time by adding the travel time between the cities.
current_time += distances[current_city, next_city]
# The objective is to minimize the time at which the tour finishes.
return current_time
Next, we generate a random problem instance with time windows and compile this function into a Gurobi model using compile_from_python():
P_val = causara.Demos.TSP_with_time_windows.generate_P(3, num_cities=15, num_cities_with_time_window=5)
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_with_time_windows")
compiledGurobiModel.compile_from_python(
func=TSP_with_time_windows,
sense=GRB.MINIMIZE,
P_val=P_val,
target_vars=["route"],
forceNewCompiling=True,
num_trials=2
)
Finally, we solve one of the generated problem instances and print the resulting route, along with the objective value (the finishing time).
Complete Code
from causara import *
import causara
from gurobipy import GRB
def TSP_with_time_windows(p, c, x):
distances = p["distances"]
num_cities = p["num_cities"]
time_window_start = p["time_window_start"]
time_window_end = p["time_window_end"]
# Define the route as a decision variable that assigns a city to each position.
route = Var(num_cities, Types.INTEGER, x, "route", lowerBound=0, upperBound=num_cities-1)
# Start the route at 8:00.
current_time = 8
# Ensure all cities are visited exactly once.
assert allDifferent(route)
# Traverse all cities in the order defined by 'route'.
for i in range(num_cities):
if i < num_cities - 1:
current_city = route[i]
next_city = route[i + 1]
else:
current_city = route[i]
next_city = route[0]
# If the current city has a time window, check feasibility.
if time_window_start[current_city] != -1:
if current_time < time_window_start[current_city] or current_time > time_window_end[current_city]:
error()
# Update the current time with travel time.
current_time += distances[current_city, next_city]
# Minimize total completion time.
return current_time
# Generate a random problem instance with time windows.
P_val = causara.Demos.TSP_with_time_windows.generate_P(3, num_cities=15, num_cities_with_time_window=5)
# Compile the function into a Gurobi model.
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_with_time_windows")
compiledGurobiModel.compile_from_python(
func=TSP_with_time_windows,
sense=GRB.MINIMIZE,
P_val=P_val,
target_vars=["route"],
forceNewCompiling=True,
num_trials=2
)
# Solve a selected instance.
p = P_val.iloc[0]
x, _, obj_value = compiledGurobiModel.solve(p)[0]
print(f"\nObjective value: {obj_value}\n")
route = x["route"]
print(f"Route: {route}")
Post-Processing
In many real-world optimization problems, it is extremely challenging to capture every nuance or detail in the mathematical formulation. Gurobi models are often simplified representations that approximate the original problem. Consequently, some real-world constraints or objectives might be only loosely modeled. Post-processing is necessary to refine the solutions obtained from the Gurobi model, ensuring that they better match the true requirements of the problem.
For instance, in the following cell tower placement demo, the Gurobi model uses simplifying assumptions to make the problem tractable. Post-processing allows us to re-evaluate and adjust the solutions using a more detailed and realistic evaluation function.
post_processing_with_python(func, c_post)
func: Any Python function with parameters(p, c, x)that returns a scalar value. This function computes a refined objective function that better captures the real-world performance of the solution.c_post: A dictionary containing constant parameters required by the post-processing function. Useful when you want to further fine-tune the post-processing function on real-world data.
In the following, we present a demo on how to use this feature.
Cell Tower Placement
In this demo, we are given a map that specifies the desired cell coverage over an area. Our goal is to decide where to place cell towers such that the desired coverage is achieved while minimizing the total number of towers. This optimization problem is very complex and cannot be solved exactly, so we make two key simplifying assumptions:
First Simplification: We assume that the cell coverage of a tower is a rectangle around the tower rather than a circle. Although in reality the coverage is circular, using a rectangular approximation simplifies the constraints and makes the problem more tractable.
Second Simplification: We coarsen the resolution of the coverage map. Instead of working with a very fine grid that represents the real area, we aggregate cells into larger “coarse” cells. This reduces the problem size and further simplifies the model. The number 0, 1, 2, ... represents the number of cell towers that should be reachable from this cell.
Using these adjustments, we can formulate a Gurobi model that minimizes the number of cell towers while ensuring that each coarse cell receives at least the desired amount of coverage. However, because these assumptions are simplifications, the solution from the Gurobi model may not perfectly meet the original high-resolution and circular coverage requirements. To address this, we use post-processing to evaluate the solution more accurately.
The Gurobi model with the simplifying assumptions is:
def gurobi(p, c):
desired_coverage_coarse = p["desired_coverage_coarse"]
size = p["size"]
model = gp.Model()
# Decision variable: whether to place a cell tower in a given coarse cell.
cell_towers = model.addVars(size, size, vtype=GRB.BINARY, name='cell_towers')
# Coverage: number of towers that can serve a given coarse cell.
coverage = model.addVars(size, size, vtype=GRB.INTEGER, name='coverage')
# For each cell, count the number of towers in its square neighborhood (with a radius of 3 cells).
for i in range(size):
for j in range(size):
neighborhood = [cell_towers[k, l]
for k in range(max(0, i-3), min(size, i+3+1))
for l in range(max(0, j-3), min(size, j+3+1))]
model.addConstr(coverage[i, j] == gp.quicksum(neighborhood), name=f"coverage_{i}_{j}")
# Ensure that the coverage in each cell is at least the desired coverage.
for i in range(size):
for j in range(size):
model.addConstr(coverage[i, j] >= desired_coverage_coarse[i][j], name=f"min_cov_{i}_{j}")
# Objective: minimize the total number of cell towers.
model.setObjective(gp.quicksum(cell_towers[i, j] for i in range(size) for j in range(size)), GRB.MINIMIZE)
return model
We will now use compile_from_gurobi() as we have already seen in the Quickstart section.
P_test = causara.Demos.Cell_tower.generate_P(n=10, size=20)
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="cell_towers")
compiledGurobiModel.compile_from_gurobi(func=gurobi, c={}, target_vars=["cell_towers"], sense=GRB.MINIMIZE)
mean_insufficient_cell_coverage = evaluate(compiledGurobiModel, P_test)
While this Gurobi model uses the coarse grid and rectangular coverage assumptions, we can improve the quality of the solution using post-processing. In the post-processing step, we evaluate each solution on a finer resolution grid and with circular coverage to compute a more realistic measure of insufficient coverage.
The post-processing function must have three parameters (p, c, x) and must return a scalar value.
Here, we calculate the number of cells in the fine-resolution grid with insufficient cell coverage.
def post_processing(p, c, x):
desired_coverage = p["desired_coverage"]
size = p["size"]
cell_towers = x["cell_towers"]
# Convert coarse cell tower placements to positions on a fine grid (10 times finer resolution).
fine_size = size * 10
tower_positions = []
for i in range(size):
for j in range(size):
if cell_towers[i][j] == 1:
# Compute the center of the coarse cell in the fine grid.
tower_positions.append((i * 10 + 5, j * 10 + 5))
# Compute the coverage on the fine grid using circular coverage areas.
coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
for tower_x, tower_y in tower_positions:
distance = np.sqrt((i - tower_x)**2 + (j - tower_y)**2)
if distance <= 40: # A radius of 40 on the fine grid approximates a radius of 4 on the coarse grid.
coverage[i][j] += 1
# Count the number of fine grid cells where the actual coverage is below the desired coverage.
insufficient_cell_coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
if coverage[i][j] < desired_coverage[i][j]:
insufficient_cell_coverage[i][j] = 1
return np.sum(insufficient_cell_coverage)
We then add this post-processing function to our compiled model using post_processing_with_python().
This allows the system to evaluate the solution with the detailed objective function defined above.
compiledGurobiModel.post_processing_with_python(func=post_processing, c_post={})
Below is the complete code for the cell tower placement demo, including post-processing. This code first compiles the Gurobi model based on the simplified assumptions and then applies the post-processing function to assess and improve solution quality.
Complete Code
from causara import *
import causara
import gurobipy as gp
from gurobipy import GRB
import numpy as np
def gurobi(p, c):
desired_coverage_coarse = p["desired_coverage_coarse"]
size = p["size"]
model = gp.Model()
cell_towers = model.addVars(size, size, vtype=GRB.BINARY, name='cell_towers')
coverage = model.addVars(size, size, vtype=GRB.INTEGER, name='coverage')
# Calculate coverage: number of towers in a square neighborhood (radius 3) for each cell.
for i in range(size):
for j in range(size):
neighborhood = [cell_towers[k, l]
for k in range(max(0, i-3), min(size, i+3+1))
for l in range(max(0, j-3), min(size, j+3+1))]
model.addConstr(coverage[i, j] == gp.quicksum(neighborhood), name=f"coverage_{i}_{j}")
# Enforce that each cell meets the desired coverage requirement.
for i in range(size):
for j in range(size):
model.addConstr(coverage[i, j] >= desired_coverage_coarse[i][j], name=f"min_cov_{i}_{j}")
# Objective: minimize the total number of cell towers.
model.setObjective(gp.quicksum(cell_towers[i, j] for i in range(size) for j in range(size)), GRB.MINIMIZE)
return model
def post_processing(p, c, x):
desired_coverage = p["desired_coverage"]
size = p["size"]
cell_towers = x["cell_towers"]
# Convert coarse cell tower placements to fine grid positions (10x finer resolution).
fine_size = size * 10
tower_positions = []
for i in range(size):
for j in range(size):
if cell_towers[i][j] == 1:
tower_positions.append((i * 10 + 5, j * 10 + 5)) # Center of cell (i, j) in the fine grid.
# Calculate fine grid coverage using circular areas.
coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
for tower_x, tower_y in tower_positions:
distance = np.sqrt((i - tower_x)**2 + (j - tower_y)**2)
if distance <= 40: # Corresponds to a radius of 4 in the coarse grid.
coverage[i][j] += 1
# Compute the number of cells that do not meet the desired coverage.
insufficient_cell_coverage = np.zeros((fine_size, fine_size))
for i in range(fine_size):
for j in range(fine_size):
if coverage[i][j] < desired_coverage[i][j]:
insufficient_cell_coverage[i][j] = 1
return np.sum(insufficient_cell_coverage)
def evaluate(compiledGurobiModel, P_test):
insufficient_cell_coverage = []
for i in range(len(P_test)):
p = P_test.iloc[i]
data = compiledGurobiModel.create_data(p, num_solutions=20)
x = data.get_list_of_x()[0] # Select the best solution.
insufficient_cell_coverage.append(post_processing(p, {}, x))
return int(np.mean(insufficient_cell_coverage))
# Generate test problem instances.
P_test = causara.Demos.Cell_tower.generate_P(n=10, size=20)
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="cell_towers")
compiledGurobiModel.compile_from_gurobi(func=gurobi, c={}, target_vars=["cell_towers"], sense=GRB.MINIMIZE)
mean_insufficient_cell_coverage = evaluate(compiledGurobiModel, P_test)
# Apply post-processing to improve the solution evaluation.
compiledGurobiModel.post_processing_with_python(func=post_processing, c_post={})
mean_insufficient_cell_coverage_with_post_processing = evaluate(compiledGurobiModel, P_test)
data = compiledGurobiModel.create_data(P_test.iloc[0])
causara.Demos.Cell_tower.plot_coverage_map(data)
print(f"\nArea with insufficient cell coverage: {mean_insufficient_cell_coverage}")
print(f"Area with insufficient cell coverage [using Post-Processing]: {mean_insufficient_cell_coverage_with_post_processing}")
Result

Using the post-processing we reduced the area with insufficient coverage from 1431 to 1068 with the same number of cell towers.
GUI / AI-Interface for Gurobi Models
In many organizations, especially those with non-technical staff, it is essential to provide an intuitive interface for interacting with optimization models. Our AI-powered GUI enables users to easily select, start, interrupt, and review Gurobi models without writing any code. Using natural language, users can request modifications, adjustments, and even interpret the model's solutions. This no-code interface bridges the gap between complex optimization models and the end-users who rely on them for decision-making.
You can start the causara GUI using the following command:
python
>>> import causara
>>> causara.GUI()
You can also create a shortcut on the Desktop using the command:
python
>>> import causara
>>> causara.create_shortcut()
Below, we use the simple TSP model from the Quickstart section to illustrate how our system integrates with the GUI and AI interface.
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["distance"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["distance"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP")
compiledGurobiModel.compile_from_gurobi(gurobi, target_vars=["x"], c=causara.Demos.TSP_real_data.c)
Adding a README to the Model
Providing a README for your Gurobi model offers essential context and documentation, which is especially valuable when non-technical users interact with
the model via the AI interface. The README explains the meaning of the input data (p) and provides details about the decision variables.
In this demo, we describe the TSP problem, noting that p['cities'] is a binary vector where each entry indicates whether a city is
included in the route. Additionally, we list the city names for clarity. This additional context helps the AI interface understand the model better,
thereby facilitating more accurate natural language modifications and insightful solution presentations.
cities = ["Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol", "Newcastle upon Tyne", "Leicester", "Coventry",
"Bradford", "Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham", "Derby", "Southampton", "Portsmouth",
"Plymouth", "Exeter", "Norwich", "Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath", "Preston",
"Oxford", "Cambridge", "Carlisle"]
compiledGurobiModel.set_README(f"This is a classic Traveling Salesman Problem (TSP) model. The input p['cities'] is a binary vector of length 30,
where p['cities'][i] = 1 indicates that city i is to be included in the route. The model seeks a closed route (i.e., starting and ending at city 0)
that minimizes the total travel distance. The list of cities is as follows: {cities}.")
Now we can upload and save this model to the cloud, making it accessible via our GUI and AI-Interface.
compiledGurobiModel.upload()
Adding a Metric
A metric is a quantitative measure that summarizes a key aspect of your optimization model’s performance. In our context, a metric function extracts and formats information from the model's inputs and outputs, presenting the results in an easily understandable format. Metrics help users quickly grasp the quality and characteristics of a solution without having to interpret raw numerical data.
A metric function must take as inputs the three parameters (p, c, x) and return two lists
of equal size: one containing labels (a list of strings) and the other containing corresponding values. In our demo below,
the metric reconstructs the optimized route as a human-readable string by mapping the positions in the route back to city names.
This metric works as follows: It first determines which cities are selected based on the binary vector p["cities"].
Then, using the solution data in x["x"], it reconstructs the order in which these cities are visited. Finally,
it creates labels (e.g., "City 1", "City 2", etc.) and assigns the corresponding city names from a predefined list.
The result is a clear and concise description of the route.
def metric(p, c, x):
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Identify which cities are selected
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
labels = [f"City {i+1}" for i in range(n)]
values = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
return labels, values
compiledGurobiModel.add_metric("Route", metric, explanation="The optimized route as a human-readable string")
We can also create a metric using AI. With this feature, you simply provide a natural language description of what the metric should display. For example, you can request a metric that calculates the number of days required for a route if you drive a maximum of 8 hours per day and always sleep in one of the cities. The AI will then generate a metric that not only reports the total travel time divided by driving hours but also details for each day, including the city where you will sleep and the driving hours completed.
compiledGurobiModel.generate_AI_metric(user_request="Please generate a metric that prints how many days it takes for the route
if you drive max 8h per day and always sleep in one of the cities. Further tell me for each night in which city I will sleep and
after how many hours of driving during the day I arrive there. Note that I can drive 80km per hour. Example: if the route is
'City A' -> 'City B' -> ... -> 'City A', then the schedule could look something like: Day 1: 'City E' after <> hours.
Day 2: 'City J' after <> hours. ... 'City A' after <> hours.")
compiledGurobiModel.print_all_metric_names()
compiledGurobiModel.upload()
When you run this model in the GUI and click on "Summary," an Excel spreadsheet will open displaying the metrics for each solution.
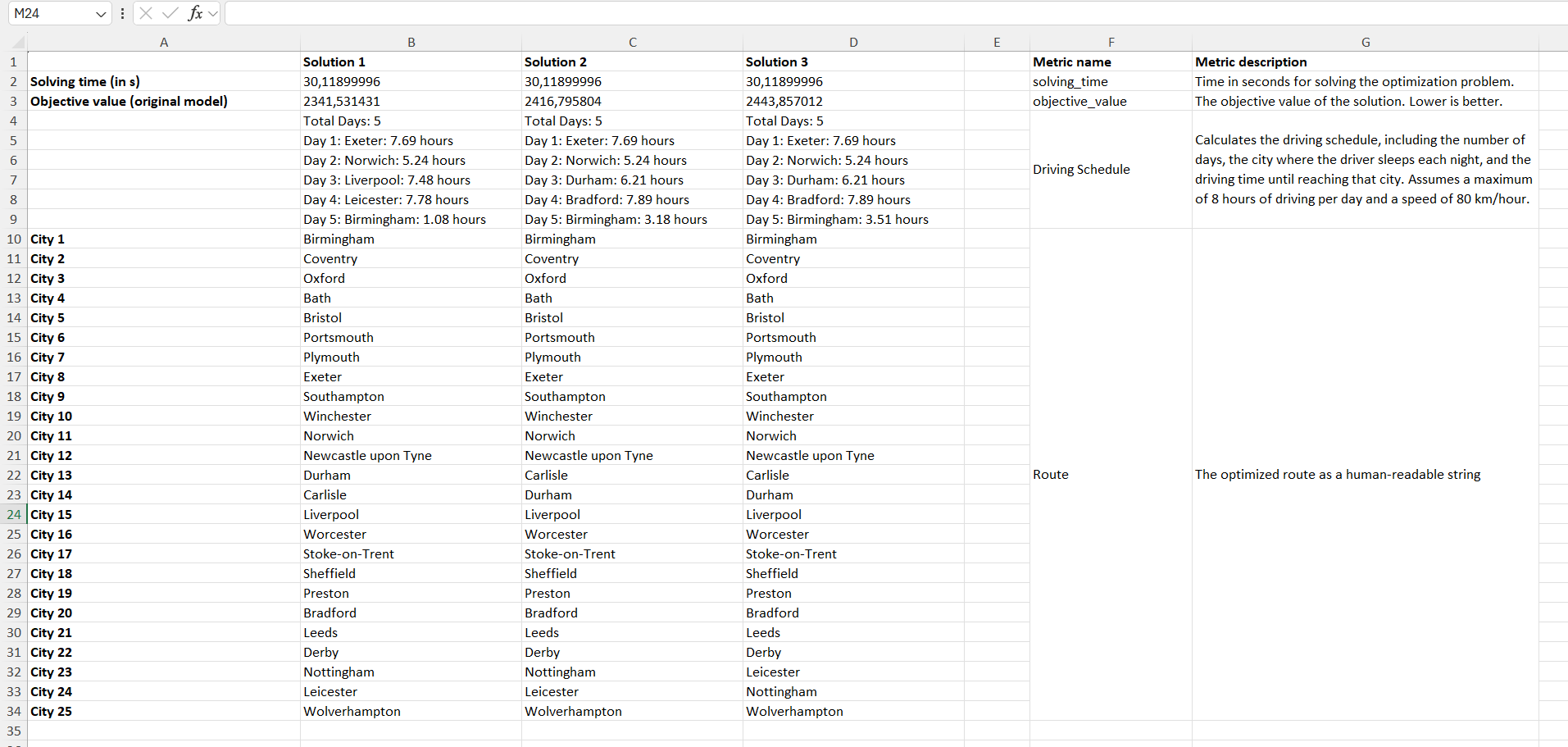
In the screenshot, you can see the summary generated by the GUI. Our custom metric, named "Route", displays the optimized tour in a clear, human-readable format by showing which city is visited at each position along the route. In addition, the AI-generated metric "Driving Schedule" provides an estimated travel schedule: it calculates the number of days required to complete the tour under the constraints of driving at a maximum speed of 80 km/h and no more than 8 hours per day. This metric details, for each day, the city where you would stop for the night along with the total driving hours for that day.
Adding Scripts
You can enhance your model by adding four types of custom scripts. These scripts enable you to integrate external data, visualize results, export solutions, and compute real-world objective values.
-
read(): A custom Python function that retrieves a problem instance (p). For example, it may extract data from a SQL database or read it from a file. -
view(p, c, x): A function for representing or visualizing the solution in a user-friendly manner. -
write(p, c, x): A function that writes the solution back into other parts of your IT systems, such as storing it in a database or sending an email notification. -
objective(p, c, x): A function that computes and retrieves a real-world objective value for a given solutionx.
Below is a demonstration of how to integrate custom scripts into our TSP Gurobi model:
-
read(): This script retrieves a problem instance. In the demo, it randomly generates a binary vector indicating which cities are to be included in the route. -
view(p, c, x): This script visualizes the solution. It uses the Folium library to create a map that displays the route. The function reconstructs the route from the solution variables, retrieves the corresponding coordinates for each city, and then adds markers and a connecting polyline to the map. -
write(p, c, x): This script is designed for processing and storing the selected solution. In a real-world application, you might use it to write the solution back into a database or send notifications via email. -
objective(p, c, x): This script fetches the actual objective value from external IT systems. For demonstration purposes, it simply returns the value42.
After defining these scripts, they are added to the compiled Gurobi model. Finally, the model is uploaded to the cloud, making it accessible via the GUI.
def read():
# Create a random problem instance with 20 cities in the route
arr = np.array([1] * 20 + [0] * 10)
np.random.shuffle(arr)
p = {"cities": arr}
return p
def view(p, c, x):
import folium
import webbrowser
import os
from pathlib import Path
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Verified hard-coded coordinates (latitude, longitude)
city_coords = {
"Birmingham": (52.48142, -1.89983),
"Leeds": (53.79648, -1.54785),
"Sheffield": (53.38297, -1.46590),
"Manchester": (53.48095, -2.23743),
"Liverpool": (53.41058, -2.97794),
"Bristol": (51.45523, -2.59665),
"Newcastle upon Tyne": (54.97328, -1.61396),
"Leicester": (52.63860, -1.13169),
"Coventry": (52.40656, -1.51217),
"Bradford": (53.79391, -1.75206),
"Kingston upon Hull": (53.74460, -0.33525),
"Stoke-on-Trent": (53.00415, -2.18538),
"Wolverhampton": (52.58547, -2.12296),
"Nottingham": (52.95360, -1.15047),
"Derby": (52.92277, -1.47663),
"Southampton": (50.90395, -1.40428),
"Portsmouth": (50.79899, -1.09125),
"Plymouth": (50.37153, -4.14305),
"Exeter": (50.72360, -3.52751),
"Norwich": (52.62783, 1.29834),
"Chester": (53.19050, -2.89189),
"Durham": (54.77676, -1.57566),
"Winchester": (51.06513, -1.31870),
"Gloucester": (51.86568, -2.24310),
"Worcester": (52.18935, -2.22001),
"Bath": (51.37510, -2.36172),
"Preston": (53.76282, -2.70452),
"Oxford": (51.75222, -1.25596),
"Cambridge": (52.20000, 0.11667),
"Carlisle": (54.89510, -2.93820)
}
# Identify which cities are selected based on p["cities"]
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
# Build the route using the selected cities and their order
route = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
route.append(route[0]) # Complete the circuit by returning to the start
# Retrieve coordinates from the hard-coded dictionary
coordinates = []
for city in route:
if city in city_coords:
coordinates.append(city_coords[city])
else:
print(f"Could not find coordinates for {city}")
if not coordinates:
print("No coordinates found. Exiting.")
return
# Create a folium map centered on the first city
m = folium.Map(location=coordinates[0], zoom_start=6)
# Add markers for each city along the route
for i, (lat, lon) in enumerate(coordinates):
folium.Marker([lat, lon], popup=route[i]).add_to(m)
# Draw a polyline connecting the cities in the order of the route
folium.PolyLine(locations=coordinates, color="blue", weight=2.5, opacity=1).add_to(m)
file_name = "map.html"
documents_folder = Path.home() / "Documents"
documents_folder.mkdir(parents=True, exist_ok=True)
html_file = documents_folder / file_name
print(html_file)
m.save(html_file)
# Convert the relative path to an absolute file URL
file_path = os.path.abspath(html_file)
file_url = "file://" + file_path
webbrowser.open(file_url)
def write(p, c, x):
print("Processing and storing the chosen solution x with your own code.")
def objective(p, c, x):
print("Retrieving the actual objective value from external IT sources.")
return 42 # For demonstration purposes, returns 42
compiledGurobiModel.add_read_script(read)
compiledGurobiModel.add_view_script(view)
compiledGurobiModel.add_write_script(write)
compiledGurobiModel.add_objective_script(objective)
compiledGurobiModel.upload()
Video Tutorial
This is the complete code from all four previous sections including a README, a custom metric, an AI-generated metric and scripts for read,
view, write and objective. The video tutorial below uses the model created with this code.
from causara import *
import gurobipy as gp
from gurobipy import GRB
import causara
import numpy as np
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["distance"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["distance"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
def metric(p, c, x):
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Identify which cities are selected
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
labels = [f"City {i+1}" for i in range(n)]
values = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
return labels, values
def read():
# Create a random problem instance with 20 cities in the route
arr = np.array([1] * 20 + [0] * 10)
np.random.shuffle(arr)
p = {"cities": arr}
return p
def view(p, c, x):
import folium
import webbrowser
import os
from pathlib import Path
all_city_names = [
"Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol",
"Newcastle upon Tyne", "Leicester", "Coventry", "Bradford",
"Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham",
"Derby", "Southampton", "Portsmouth", "Plymouth", "Exeter", "Norwich",
"Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath",
"Preston", "Oxford", "Cambridge", "Carlisle"
]
# Verified hard-coded coordinates (latitude, longitude)
city_coords = {
"Birmingham": (52.48142, -1.89983),
"Leeds": (53.79648, -1.54785),
"Sheffield": (53.38297, -1.46590),
"Manchester": (53.48095, -2.23743),
"Liverpool": (53.41058, -2.97794),
"Bristol": (51.45523, -2.59665),
"Newcastle upon Tyne": (54.97328, -1.61396),
"Leicester": (52.63860, -1.13169),
"Coventry": (52.40656, -1.51217),
"Bradford": (53.79391, -1.75206),
"Kingston upon Hull": (53.74460, -0.33525),
"Stoke-on-Trent": (53.00415, -2.18538),
"Wolverhampton": (52.58547, -2.12296),
"Nottingham": (52.95360, -1.15047),
"Derby": (52.92277, -1.47663),
"Southampton": (50.90395, -1.40428),
"Portsmouth": (50.79899, -1.09125),
"Plymouth": (50.37153, -4.14305),
"Exeter": (50.72360, -3.52751),
"Norwich": (52.62783, 1.29834),
"Chester": (53.19050, -2.89189),
"Durham": (54.77676, -1.57566),
"Winchester": (51.06513, -1.31870),
"Gloucester": (51.86568, -2.24310),
"Worcester": (52.18935, -2.22001),
"Bath": (51.37510, -2.36172),
"Preston": (53.76282, -2.70452),
"Oxford": (51.75222, -1.25596),
"Cambridge": (52.20000, 0.11667),
"Carlisle": (54.89510, -2.93820)
}
# Identify which cities are selected based on p["cities"]
selected_indices = [i for i in range(len(all_city_names)) if p["cities"][i] == 1]
n = len(selected_indices)
# Reconstruct the route based on x["x"]
route_positions = [None] * n
for city_idx in range(n):
for pos in range(n):
if x["x"][city_idx, pos] > 0.5:
route_positions[pos] = city_idx
break
# Build the route using the selected cities and their order
route = [all_city_names[selected_indices[city_idx]] for city_idx in route_positions]
route.append(route[0]) # Complete the circuit by returning to the start
# Retrieve coordinates from the hard-coded dictionary
coordinates = []
for city in route:
if city in city_coords:
coordinates.append(city_coords[city])
else:
print(f"Could not find coordinates for {city}")
if not coordinates:
print("No coordinates found. Exiting.")
return
# Create a folium map centered on the first city
m = folium.Map(location=coordinates[0], zoom_start=6)
# Add markers for each city along the route
for i, (lat, lon) in enumerate(coordinates):
folium.Marker([lat, lon], popup=route[i]).add_to(m)
# Draw a polyline connecting the cities in the order of the route
folium.PolyLine(locations=coordinates, color="blue", weight=2.5, opacity=1).add_to(m)
file_name = "map.html"
documents_folder = Path.home() / "Documents"
documents_folder.mkdir(parents=True, exist_ok=True)
html_file = documents_folder / file_name
print(html_file)
m.save(html_file)
# Convert the relative path to an absolute file URL
file_path = os.path.abspath(html_file)
file_url = "file://" + file_path
webbrowser.open(file_url)
def write(p, c, x):
print("Processing and storing the chosen solution x with your own code.")
def objective(p, c, x):
print("Retrieving the actual objective value from external IT sources.")
return 42 # For demonstration purposes, returns 42
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_Tutorial")
compiledGurobiModel.compile_from_gurobi(gurobi, target_vars=["x"], c=causara.Demos.TSP_real_data.c)
compiledGurobiModel.set_default_time_limit(time_limit=60)
cities = ["Birmingham", "Leeds", "Sheffield", "Manchester", "Liverpool", "Bristol", "Newcastle upon Tyne", "Leicester", "Coventry",
"Bradford", "Kingston upon Hull", "Stoke-on-Trent", "Wolverhampton", "Nottingham", "Derby", "Southampton", "Portsmouth",
"Plymouth", "Exeter", "Norwich", "Chester", "Durham", "Winchester", "Gloucester", "Worcester", "Bath", "Preston",
"Oxford", "Cambridge", "Carlisle"]
compiledGurobiModel.set_README(f"This is a classic TSP problem. p['cities'] is a binary vector of length 30 where p['cities'][i] = 1 indicates that city i should be part of the route. "
f"The cities are: {cities}. The route must be closed, so always consider the time going from the last city back to the first city.")
compiledGurobiModel.generate_AI_metric(user_request="Please generate a metric that prints how many days it takes for the route if you drive max 8h per day and always sleep in "
"one of the cities. Further tell me for each night in which city I will sleep and after how many hours of driving during the "
"day I arrive there. Note that I can drive 80km per hour. Example: if the route is 'City A' -> 'City B' -> ... -> "
"'City A', then the schedule could look something like: Day 1: 'City E' after <> hours. Day 2: 'City J' after <> hours. ... 'City A' "
"after <> hours.")
compiledGurobiModel.add_metric("Route", metric, explanation="The optimized route as a human-readable string")
compiledGurobiModel.print_all_metric_names()
compiledGurobiModel.add_read_script(read)
compiledGurobiModel.add_view_script(view)
compiledGurobiModel.add_write_script(write)
compiledGurobiModel.add_objective_script(objective)
compiledGurobiModel.upload()
You can start the causara GUI using the following command:
python
>>> import causara
>>> causara.GUI()
You can also create a shortcut on the Desktop using the command:
python
>>> import causara
>>> causara.create_shortcut()
Fine-tuning
Fine-tuning is the process of refining a compiled Gurobi model so that it better matches real-world performance. Even though an initial model may be a good approximation, real-world data often contains complexities and variations that are not fully captured in the initial formulation.
finetuning_model(real_world_data, params={}, n_additional=100, solving_time=10.0, num_repetitions=2, var="")
real_world_data: A Real_World_Data object that contains real-world objective values.params: parameters for the neural network that updates the Gurobi model.n_additional: number of additional solutions for contrastive learning. The higher, the better but the longer the optimization will take.solving_time: solving time for Gurobi models within the training procedure.num_repetitions: number of repetitions the training shall be performed. The higher, the better but the longer the optimization will take.var: the variable name to be optimized (must be one of the variables intarget_vars.
finetuning_constants(real_world_data, bounds_gurobi=None, bounds_postprocessing=None, mode='obj_val', save_aux_vars=False, batchSize=10000, nEpochs=1000, numSteps=5)
real_world_data: A Real_World_Data object that contains real-world objective values.bounds_gurobi: A Bounds object or None. A Bounds object that specifies which constants of the Gurobi model to fine-tune and within which bounds of the initial values.bounds_postprocessing: A Bounds object or None. A Bounds object that specifies which constants of the Post-Processing function to fine-tune and within which bounds of the initial values.mode: Must be either'obj_val'or'pref'. With'obj_val'fine-tuning is performed on the provided real-world objective values. With'pref'fine-tuning is performed on the human preference. Given a set of solutions: a human chose the best option. The fine-tuning procedure will try to mimic this decision-making process.save_aux_vars: A boolean. ChooseFalsein this version of causara.batchSize: Batch size for the training procedure.nEpochs: Number of epochs to fine-tune the model.numSteps: Granularity of the optimization. The higher, the more accurate the solution can get but the optimization process will take longer.
Fine-tuning Constants
In this demo, we revisit the TSP model defined in the Quickstart section and compile it using compile_from_gurobi().
The goal here is to fine-tune the constant parameters c, in this case the duration matrix, so that the model’s predicted route
duration aligns more closely with real-world observations.
We first define the Gurobi model function as previously:
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["duration"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["duration"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
c = causara.Demos.TSP.get_initial_guess()
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_Finetuned")
compiledGurobiModel.compile_from_gurobi(func=gurobi, c=c, target_vars=["x"], sense=GRB.MINIMIZE)
Next, we need to sample real-world data. We generate training and test problem instances and simulate the real-world objective for each solution. This simulation mimics actual performance metrics that you might obtain from field data or detailed simulations.
P_train = causara.Demos.TSP.generate_P(n=200, sizes=[8])
P_test = causara.Demos.TSP.generate_P(n=50, sizes=[8])
real_world_data = Real_World_Data()
for i in range(len(P_train)):
# solve p
p = P_train.iloc[i]
data = compiledGurobiModel.create_data(p, num_solutions=1)
# we choose solution 0 (the solution with the highest objective value)
data.set_chosen_idx(0)
# we simulate the real-world objective for this solution (could also be retrieved manually)
real_world_obj_value = causara.Demos.TSP.simulate_real_world(p, data.get_chosen_x())
data.set_rw_obj_value(real_world_obj_value)
# store this Data object in the Real_World_Data object
real_world_data.append(data)
print(real_world_data)
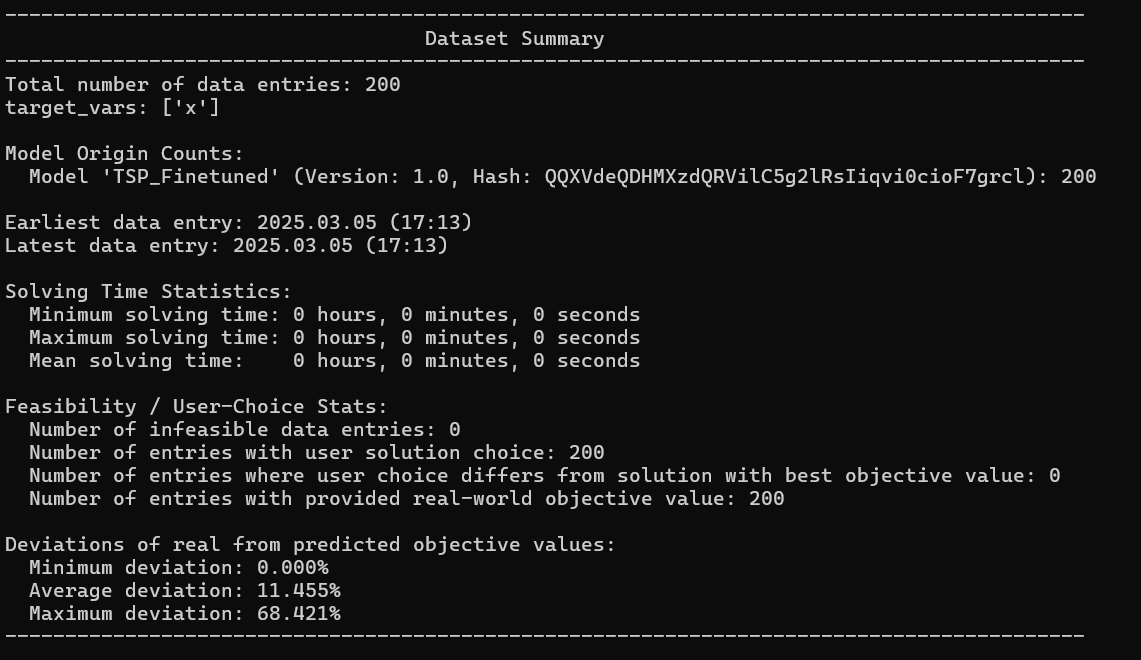
Now, we define bounds for our constants. These bounds specify the range within which the optimized constant parameters should lie relative to their initial values. In this demo, we allow the duration values to vary between 60% and 140% of their initial guess.
bounds = Bounds(c)
bounds.add_relative_deviation_bound("duration", 0.6, 1.4) # search within the 60% until 140% interval relative to the initial values of c
compiledGurobiModel.finetuning_constants(real_world_data, bounds_gurobi=bounds, batchSize=100, nEpochs=600)
After fine-tuning, we evaluate the model again on the test set to measure the improvement in the mean route duration.
mean_duration = evaluate(compiledGurobiModel, P_test)
print(f"Mean route duration before fine-tuning: {mean_duration}")
print(f"Mean route duration after fine-tuning: {mean_duration_finetuned}")
Complete Code
from causara import *
import causara
import gurobipy as gp
from gurobipy import GRB
def gurobi(p, c):
selected_cities = [i for i in range(len(p["cities"])) if p["cities"][i] == 1]
n = len(selected_cities)
model = gp.Model()
x = model.addVars(n, n, vtype=GRB.BINARY, name='x')
for i in range(n):
model.addConstr(gp.quicksum(x[i, j] for j in range(n)) == 1) # to every city a position in the route is assgined
model.addConstr(gp.quicksum(x[j, i] for j in range(n)) == 1) # to every position in the route a city is assigned
model.addConstr(x[0, 0] == 1) # city 0 is at position 0 (and n-1)
objective = 0
for city1 in range(n):
c1 = selected_cities[city1]
for position_city1 in range(n):
for city2 in range(n):
c2 = selected_cities[city2]
for position_city2 in range(n):
if position_city2 == position_city1 + 1:
objective += c["duration"][c1][c2] * x[city1, position_city1] * x[city2, position_city2]
if position_city1 == 0 and position_city2 == n - 1:
objective += c["duration"][c1][c2] * x[city1, position_city2] * x[city2, position_city1]
model.setObjective(objective, GRB.MINIMIZE)
return model
def evaluate(compiledGurobiModel, P_test):
mean_duration = 0
for i in range(len(P_test)):
p = P_test.iloc[i]
data = compiledGurobiModel.create_data(p, num_solutions=1)
x = data.get_list_of_x()[0] # choose the best solution according to the current model
mean_duration += causara.Demos.TSP.simulate_real_world(p, x)
return mean_duration / len(P_test)
c = causara.Demos.TSP.get_initial_guess()
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP_Finetuned")
compiledGurobiModel.compile_from_gurobi(func=gurobi, c=c, target_vars=["x"], sense=GRB.MINIMIZE)
P_train = causara.Demos.TSP.generate_P(n=200, sizes=[8])
P_test = causara.Demos.TSP.generate_P(n=50, sizes=[8])
mean_duration = evaluate(compiledGurobiModel, P_test)
real_world_data = Real_World_Data()
for i in range(len(P_train)):
# solve p
p = P_train.iloc[i]
data = compiledGurobiModel.create_data(p, num_solutions=1)
# we choose solution 0 (the solution with the highest objective value)
data.set_chosen_idx(0)
# we simulate the real-world objective for this solution (could also be retrieved manually)
real_world_obj_value = causara.Demos.TSP.simulate_real_world(p, data.get_chosen_x())
data.set_rw_obj_value(real_world_obj_value)
# store this Data object in the Real_World_Data object
real_world_data.append(data)
print(real_world_data)
bounds = Bounds(c)
bounds.add_relative_deviation_bound("duration", 0.6, 1.4) # search within the 60% until 140% interval relative to the initial values of c
compiledGurobiModel.finetuning_constants(real_world_data, bounds_gurobi=bounds, batchSize=100, nEpochs=600)
mean_duration_finetuned = evaluate(compiledGurobiModel, P_test)
print(f"Mean route duration before fine-tuning: {mean_duration}")
print(f"Mean route duration after fine-tuning: {mean_duration_finetuned}")
Fine-tuning the Model
Fine-tuning involves adjusting the entire model so that its outputs better reflect real-world performance. While initially you may only fine-tune the constant parameters, fine-tuning the full model typically requires more data and can lead to significant improvements. In this demo, we illustrate the process using a Shift-Scheduling Problem that incorporates employee preferences.
Fine-tuning a Shift-Scheduling and Employee Preferences Model
A Shift-Scheduling Problem is an optimization task where employees are assigned work shifts over a planning period while satisfying various constraints. In our example, the model ensures that:
- Each day has a minimum number of employees scheduled (to meet operational requirements).
- Each employee works exactly a predetermined number of days during the scheduling period.
The provided Gurobi function defines this problem. It creates binary decision variables to indicate whether an employee works on a given day and imposes two sets of constraints: one ensuring sufficient staffing each day, and another ensuring that each employee works the required number of days. The objective is set to 0 (with maximization) since this demo focuses on meeting the constraints.
from causara import *
import causara
import gurobipy as gp
from gurobipy import GRB
def gurobi(p, c):
min_employees = p["min_employees"] # numpy array of shape (14,) with min employees required per day
working_days_per_employee = p["working_days_per_employee"] # numpy array of shape (5,) with required working days per employee
model = gp.Model()
num_days = len(min_employees) # 14 days
num_employees = len(working_days_per_employee) # 5 employees
# Decision variables: x[d, i] = 1 if employee i works on day d, 0 otherwise.
x = model.addVars(num_days, num_employees, vtype=gp.GRB.BINARY, name="schedule")
# Constraint 1: For each day, at least the required number of employees must work.
for d in range(num_days):
model.addConstr(gp.quicksum(x[d, i] for i in range(num_employees)) >= min_employees[d], name=f"min_employees_day_{d}")
# Constraint 2: For each employee, they must work exactly the number of days specified.
for i in range(num_employees):
model.addConstr(gp.quicksum(x[d, i] for d in range(num_days)) == working_days_per_employee[i], name=f"working_days_employee_{i}")
model.setObjective(0, GRB.MAXIMIZE)
return model
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Shift Scheduling")
compiledGurobiModel.compile_from_gurobi(func=gurobi, target_vars=["schedule"], sense=GRB.MAXIMIZE)
Next, we generate real-world data. In this context, real-world data represents employee preferences for different shift schedules. Employees rank how much they like various schedules, and these rankings are used to simulate the true, external objective of the schedule. This data is crucial for fine-tuning because it allows the model to adjust its parameters to better align with employee satisfaction.
P_train = causara.Demos.ShiftScheduling.generate_P(n=100)
P_test = causara.Demos.ShiftScheduling.generate_P(n=10)
real_world_data = causara.Demos.ShiftScheduling.create_real_world_data(compiledGurobiModel, P_train)
print(real_world_data)
Finally, we fine-tune our model using the collected real-world data. Fine-tuning adjusts the model’s parameters so that the schedules it produces more accurately reflect the preferences of the employees while still satisfying all constraints.
params = {'nHiddens': [32], 'batchSize': 500, 'lr': 0.001, 'train_val_split': 0.8, 'nEpochs': 50, 'val_freq': 5}
compiledGurobiModel.finetuning_model(real_world_data, params=params, n_additional=1000, solving_time=10.0, num_repetitions=3)
Complete Code
from causara import *
import causara
import gurobipy as gp
from gurobipy import GRB
def gurobi(p, c):
min_employees = p["min_employees"] # numpy array of shape (14,) with min employees required per day
working_days_per_employee = p["working_days_per_employee"] # numpy array of shape (5,) with required working days per employee
model = gp.Model()
num_days = len(min_employees) # 14 days
num_employees = len(working_days_per_employee) # 5 employees
# Decision variables: x[d, i] = 1 if employee i works on day d, 0 otherwise.
x = model.addVars(num_days, num_employees, vtype=gp.GRB.BINARY, name="schedule")
# Constraint 1: For each day, at least the required number of employees must work.
for d in range(num_days):
model.addConstr(gp.quicksum(x[d, i] for i in range(num_employees)) >= min_employees[d], name=f"min_employees_day_{d}")
# Constraint 2: For each employee, they must work exactly the number of days specified.
for i in range(num_employees):
model.addConstr(gp.quicksum(x[d, i] for d in range(num_days)) == working_days_per_employee[i], name=f"working_days_employee_{i}")
model.setObjective(0, GRB.MAXIMIZE)
return model
def evaluate(compiledGurobiModel, P_test):
mean_pref = 0
for i in range(len(P_test)):
p = P_test.iloc[i]
x = compiledGurobiModel.create_data(p, num_solutions=1).get_list_of_x()[0]
mean_pref += causara.Demos.ShiftScheduling.team_preference(p, x)
mean_pref /= len(P_test)
return mean_pref
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="Shift Scheduling")
compiledGurobiModel.compile_from_gurobi(func=gurobi, target_vars=["schedule"], sense=GRB.MAXIMIZE)
P_train = causara.Demos.ShiftScheduling.generate_P(n=100)
P_test = causara.Demos.ShiftScheduling.generate_P(n=10)
real_world_data = causara.Demos.ShiftScheduling.create_real_world_data(compiledGurobiModel, P_train)
print(real_world_data)
mean_pref = evaluate(compiledGurobiModel, P_test)
params = {'nHiddens': [32], 'batchSize': 500, 'lr': 0.001, 'train_val_split': 0.8, 'nEpochs': 50, 'val_freq': 5}
compiledGurobiModel.finetuning_model(real_world_data, params=params, n_additional=1000, solving_time=10.0, num_repetitions=3)
mean_pref_finetuned = evaluate(compiledGurobiModel, P_test)
print(f"Mean employee preference before fine-tuning: {mean_pref}")
print(f"Mean employee preference after fine-tuning: {mean_pref_finetuned}")
Managing Your Account
This section provides comprehensive instructions on how to manage your account on our platform. You can upload, download, and delete models or datasets,
and view detailed information about your account and stored models using the printInfos() function. These tools ensure that you have full control over
your optimization models and data.
For example, once you compile a model using compile_from_gurobi(), you can upload it to the cloud to securely store it and make it accessible from anywhere. Similarly, you can upload any real-world data associated with your model for later fine-tuning or evaluation.
from causara import *
compiledGurobiModel = CompiledGurobiModel(key="your_key", model_name="TSP")
compiledGurobiModel.compile_from_gurobi(gurobi, target_vars=["x"], c=causara.Demos.TSP.c_large, sense=GRB.MINIMIZE)
compiledGurobiModel.upload()
The code above compiles your TSP model and then uploads it to our cloud service. Once uploaded, you can also manage associated real-world data.
real_world_data = Real_World_Data()
for i in range(3):
data = compiledGurobiModel.create_data(P.iloc[i])
real_world_data.append(data)
real_world_data.upload("your_key", "TSP")
To check your account details and view the status of your uploaded models or datasets, use the printInfos() function.
This function prints important metadata such as available models / datasets, API usage and remaining tokens.
printInfos(key="your_key")
If you need to retrieve your stored model or dataset, you can download it from the cloud. This functionality allows you to restore or further process your data locally.
real_world_data = Real_World_Data()
real_world_data.download("your_key", "TSP")
print(real_world_data)
Finally, when a model or dataset is no longer required, you can permanently remove it from the cloud using the deleteModel() and deleteDataset() functions.
deleteModel(key="your_key", name="TSP")
deleteDataset(key="your_key", name="TSP")
printInfos(key="your_key")
CompiledGurobiModel
The CompiledGurobiModel class provides a comprehensive API for compiling, solving, fine-tuning, and managing Gurobi optimization models. Below is a detailed explanation of all its methods, including their parameters, return types, and expected behavior.
-
__init__(key, model_name, model_version_nr="1.0", verbose=1)
Constructor that creates a new instance of the CompiledGurobiModel.
- key (str): Your unique account key.
- model_name (str): A non-empty string representing the name of the model.
- model_version_nr (str): A version number as a string (default: "1.0").
- verbose (int): Verbosity level
-
set_default_time_limit(time_limit)
Sets the default time limit (in seconds) for solving the optimization model.
- time_limit (int or float): A number greater than 0 specifying the time limit.
- Return: None
-
set_default_useInternalSolver(useInternalSolver)
Configures whether to use the internal solver by default.
- useInternalSolver (bool): True to use the internal solver, False otherwise.
- Return: None
-
set_README(text)
Sets a README description for the model, providing additional context and documentation.
- text (str): A string containing the README details.
- Return: None
-
set_model_name(model_name)
Updates the model name.
- model_name (str): The new model name.
- Return: None
-
set_model_version_nr(model_version_nr)
Sets the model version number.
- model_version_nr (str): A string representing the version.
- Return: None
-
set_verbose(verbose)
Configures the verbosity level.
- verbose (int): Must be one of 0, 1 or 2
- Return: None
-
set_target_vars(target_vars)
Specifies the list of decision variable names for retrieve the solution.
- target_vars (list of str): A non-empty list of variable names.
- Return: None
-
get_default_time_limit()
Retrieves the default time limit.
- Return: A number (int or float) representing the time limit in seconds.
-
get_default_useInternalSolver()
Returns whether the internal solver is set by default.
- Return: A boolean value.
-
get_README()
Retrieves the README text for the model.
- Return: A string.
-
get_model_name()
Returns the model's name.
- Return: A string.
-
get_model_version_nr()
Retrieves the model version number.
- Return: A string.
-
get_verbose()
Returns the current verbosity level.
- Return: An integer.
-
get_target_vars()
Returns the list of target variable names.
- Return: A list of strings.
-
get_hash()
Generates and returns a SHA-256-based hash of the model. This can be used to verify the model’s integrity.
- Return: A 40-character string.
-
get_metrics()
Returns a dictionary of developer-generated metrics.
- Return: A dict mapping metric names to a tuple (function code, explanation).
-
get_post_processing_value(p, x)
Computes and returns the value produced by the post-processing function for a given problem instance and solution.
- p (dict or pandas Series): The problem instance.
- x (dict): The solution.
- Return: A scalar value (float) or None if post-processing is not set.
-
has_finetuning()
Indicates whether the model has been fine-tuned.
- Return: A boolean.
-
has_post_processing()
Checks if a post-processing function has been added.
- Return: A boolean.
-
is_compiled()
Determines if the model has been compiled.
- Return: A boolean (True if compiled, False otherwise).
-
get_c()
Retrieves the constant parameters (c) used in the compiled model.
- Return: A dict of constant parameters.
-
get_c_post()
Retrieves the constant parameters used in post-processing.
- Return: A dict, or an empty dict if no post-processing constants are set.
-
get_x(p, gurobi_model)
Retrieves the solution from a given problem instance and Gurobi model.
- p (dict or pandas Series): The problem instance.
- gurobi_model (gurobipy.Model): A solved Gurobi model.
- Return: A tuple (x, x_complete), where x is a dict containing only the target variables and x_complete is a dict with all solution variables.
-
get_gurobi_model(p, gurobi_params={})
Generates and returns a Gurobi model for the given problem instance using the specified solver parameters.
- p (dict or pandas Series): The problem instance.
- gurobi_params (dict): A dict of solver parameters (e.g., TimeLimit, OutputFlag).
- Return: A gurobipy.Model instance representing the optimization model for p.
-
get_obj_value(p, x)
Returns the objective value for the provided problem instance and solution.
- p (dict): The problem instance.
- x (dict): The solution.
- Return: A numeric value (int/float) representing the objective value.
-
get_obj_values(p, X)
Computes objective values for multiple solutions.
- p (dict): The problem instance.
- X (list of dicts or pandas DataFrame): A collection of solutions.
- Return: A list of numeric objective values, one for each solution.
-
compile_from_gurobi(func, target_vars, c={}, sense=None)
Compiles a Gurobi model from a Python function that defines the model using the Gurobi API.
- func (function): A Python function that takes a problem instance 'p' and constants 'c' as input, and returns a gurobipy.Model object
- target_vars (list of str): A list of variable names to retrieve from the Gurobi solution.
- c (dict): A dictionary of constant parameters for the model (default: {}).
- sense (GRB.MAXIMIZE or GRB.MINIMIZE, optional): The optimization sense. If None, it's automatically detected.
- Return: None
-
compile_from_data(P, X, P_val=None, X_val=None, params={}, categorical=False, offset=0)
Compiles a Gurobi model directly from training data. This is used for learning a model from input-output pairs.
- P (pandas.DataFrame): Training data input features.
- X (pandas.DataFrame): Training data output (the decision variables).
- P_val (pandas.DataFrame, optional): Validation data input features.
- X_val (pandas.DataFrame, optional): Validation data output variables.
- params (dict): Parameters for the data-driven model compilation.
- Return: None
-
compile_from_python(func, sense, P_val, target_vars=None, c={}, forceNewCompiling=False, num_trials=1)
Compiles a Gurobi model from a Python function that describes how to generate the Gurobi model *given a problem instance*.
- func (function): A Python function that takes a problem instance 'p' and constant parameters 'c' as input, and returns a numeric value (the objective value).
- sense (GRB.MAXIMIZE or GRB.MINIMIZE): The optimization sense.
- P_val (pandas.DataFrame): Validation data used to verify the correctness of the compiled Gurobi model.
- target_vars (list of str, optional): List of variable names. If None, it's automatically extracted.
- c (dict): Constant parameters for the model (default: {}).
- forceNewCompiling (bool): Forces recompilation even if the code hasn't changed (default: False).
- num_trials (int): Number of trials for generating the model (default: 1).
- Return: None
-
post_processing_with_python(func, c_post={})
Adds a post-processing step to the model using a Python function. This allows you to compute a custom objective value *after* Gurobi solves the main optimization problem.
- func (function): A Python function that takes the problem instance 'p', constants 'c', and solution 'x' as input, and returns a scalar (float) representing the post-processed objective value.
- c_post (dict): Constant parameters specific to the post-processing function (default: {}).
- Return: None
-
post_processing_with_data(real_world_data, var="")
Adds a data-driven post-processing step. This learns a post-processing function from real-world data. Requires at least 100 data entries.
- real_world_data (Real_World_Data): Real-world data containing problem instances, solutions, and (optionally) alternative solutions and objective values.
- var (str): The name of the target variable to use for post-processing (if multiple target variables exist). If only one target variable exists, this can be left empty.
- Return: None
-
finetuning_model(real_world_data, params={}, n_additional=100, solving_time=10.0, num_repetitions=2, var="")
Fine-tunes the model using real-world preference data. It requires a model compiled from Gurobi or Python code. Requires at least 25 preference data entries.
- real_world_data (Real_World_Data): Real-world data with preference information (chosen solutions among alternatives).
- params (dict): Parameters for fine-tuning.
- n_additional (int): Number of additional alternative solutions to generate for each data point (default: 100).
- solving_time (int or float): Time limit (in seconds) for generating alternative solutions (default: 10.0).
- num_repetitions (int): Number of repetitions for the preference learning process (default: 2).
- var (str): Name of the target variable array when fine-tuning preferences, in case there are multiple target variables (defaults to the first one).
- Return: None
-
finetuning_constants(real_world_data, bounds_gurobi=None, bounds_postprocessing=None, mode='obj_val', save_aux_vars=False, batchSize=10000, nEpochs=1000, numSteps=5)
Fine-tunes the model's constant parameters (either in the Gurobi model or the post-processing function) using real-world data. Can fine-tune based on preferences or objective values.
- real_world_data (Real_World_Data): Real-world data, which must contain preference information if mode='pref', or real-world objective values if mode='obj_val'.
- bounds_gurobi (Bounds, optional): Bounds for the constants in the Gurobi model.
- bounds_postprocessing (Bounds, optional): Bounds for the constants in the post-processing function.
- mode (str): 'pref' for preference-based fine-tuning, or 'obj_val' for objective-value-based fine-tuning (default: 'obj_val').
- save_aux_vars (bool): Whether to save auxiliary variables during fine-tuning (default: False).
- batchSize (int): Batch size for training (default: 10000).
- nEpochs (int): Number of training epochs (default: 1000).
- numSteps (int): Determines the granularity of the optimization process. Higher values increase the precision of the search, potentially finding better solutions, but at the cost of increased computation time.
- Return: None
-
create_data(p, num_solutions=1, gurobi_params={}, useInternalSolver=None)
Solves the model for a given problem instance and packages the results along with metadata into a Data object.
- p (dict): The problem instance.
- num_solutions (int): Number of solutions to retrieve (default is 1).
- gurobi_params (dict): Optional solver parameters.
- useInternalSolver (bool, optional): Whether to use the internal solver. Defaults to the model's setting.
- Return: A Data object containing the problem instance, list of solutions, complete solution details, constant parameters, objective values, solving time, model name, and additional metadata.
-
solve(p, num_solutions=1, gurobi_params={}, useInternalSolver=False, get_solving_time=False)
Solves the optimization problem for the given instance and returns the solution(s).
- p (dict or pandas Series): The problem instance.
- num_solutions (int): Number of solutions to retrieve.
- gurobi_params (dict): Solver parameters for Gurobi.
- useInternalSolver (bool): Whether to use the internal solver.
- get_solving_time (bool): If True, also returns the total solving time.
- Return: If get_solving_time is False, a list of tuples (x, x_complete, objective_value) for each solution; otherwise, a tuple of (list of solutions, total solving time).
-
adjust_model(user_request)
Adjusts the compiled model based on a natural language user request. This method uses an AI chat interface to suggest modifications.
- user_request (str): A description of the desired changes.
- Return: An empty string upon successful adjustment (the model is updated internally).
-
add_metric(name, func, explanation="")
Adds a custom developer-generated metric to the model.
- name (str): The name of the metric.
- func (function): A function that computes the metric. It must accept parameters (p, c, x) and return two lists (labels and values).
- explanation (str): A description of what the metric measures.
- Return: None
-
delete_all_developer_metrics()
Deletes all developer-generated metrics.
- Return: None
-
get_developer_metrics()
Retrieves all developer-generated metrics.
- Return: A dictionary mapping metric names to (function code, explanation) tuples.
-
generate_AI_metric(user_request, metric_name="", metric_description="")
Generates an AI-based metric using a natural language description and stores it.
- user_request (str): A natural language request describing what the metric should display.
- metric_name (str): Optional name for the metric.
- metric_description (str): Optional description of the metric.
- Return: None
-
delete_all_AI_metrics()
Deletes all AI-generated metrics.
- Return: None
-
get_AI_metrics()
Retrieves all AI-generated metrics.
- Return: A dictionary mapping metric names to (function code, explanation) tuples.
-
rename_metric(old_name, new_name)
Renames an existing metric.
- old_name (str): The current metric name.
- new_name (str): The new metric name.
- Return: None
-
print_all_metric_names()
Prints the names of all metrics (both developer- and AI-generated) to the console.
- Return: None
-
delete_metric(name)
Deletes a specific metric by its name.
- name (str): The name of the metric to delete.
- Return: None
-
add_read_script(func)
Adds a custom read script, used to retrieve a problem instance.
- func (function): A function that takes no parameters and returns a problem instance (p).
- Return: None
-
add_view_script(func)
Adds a custom view script for visualizing the solution.
- func (function): A function with parameters (p, c, x) that provides a visualization of the solution.
- Return: None
-
add_write_script(func)
Adds a custom write script for processing or exporting the solution.
- func (function): A function with parameters (p, c, x) that handles the output (e.g., writing to a database).
- Return: None
-
add_objective_script(func)
Adds a custom objective script to compute a real-world objective value.
- func (function): A function with parameters (p, c, x) that returns a scalar (float) representing the objective.
- Return: None
-
has_read_script()
Checks if a read script has been added.
- Return: A boolean indicating whether a read script is present.
-
has_view_script()
Checks if a view script has been added.
- Return: A boolean.
-
has_write_script()
Checks if a write script has been added.
- Return: A boolean.
-
has_objective_script()
Checks if an objective script has been added.
- Return: A boolean.
-
run_read_script()
Executes the read script and returns the problem instance.
- Return: A problem instance (dict) as returned by the read() function.
-
run_view_script(p, c, x)
Executes the view script to visualize the solution.
- p (dict): The problem instance.
- c (dict): The constants.
- x (dict): The solution.
- Return: An empty string on success, or an error message if the script fails.
-
run_write_script(p, c, x)
Executes the write script to process or export the solution.
- p (dict): The problem instance.
- c (dict): The constants.
- x (dict): The solution.
- Return: An empty string on success, or an error message if the script fails.
-
run_objective_script(p, c, x)
Executes the objective script to retrieve the real-world objective value for the solution.
- p (dict): The problem instance.
- c (dict): The constants.
- x (dict): The solution.
- Return: A float representing the objective value.
-
save(path)
Saves the compiled model to a file at the specified path.
- path (str): The file path where the model should be saved (if no ".causara_model" extension is present, it will be added).
- Return: None
-
load(path)
Loads a compiled model from a file.
- path (str): The file path from which to load the model.
- Return: None
-
upload()
Uploads the compiled model to the cloud for remote storage and management.
- Return: None
-
download()
Downloads the compiled model from the cloud and loads it into the current instance.
- Return: None
Real_World_Data
The Real_World_Data class is designed to store and manage a collection of Data objects, each of which represents a
real-world problem instance along with its computed solutions and associated metadata. This class provides methods for appending
new Data objects, merging datasets, and retrieving summarized information about the stored data.
Below is a detailed explanation of all methods, their parameters, and their return types.
-
append(data)
Appends a Data object to the collection. Before appending, it verifies that the Data object contains at least one solution and that its keys match the target variables of the existing data.
- data (Data): A Data object containing a problem instance, solution(s), and metadata.
- Return: None. If the Data object has no solutions, it is not added and a warning is issued.
-
get_target_vars()
Returns the list of target variable names that were determined from the first appended Data object.
- Return: A list of strings representing the target variable names.
-
merge(real_world_data_prev)
Merges another Real_World_Data object into the current one. It only appends Data objects from the other dataset whose problem instances are not already present.
- real_world_data_prev (Real_World_Data): Another Real_World_Data object to be merged.
- Return: None. The current Real_World_Data object is updated with non-duplicate Data objects.
-
save(path)
Saves the serialized Real_World_Data to a file. If the provided path does not have the proper extension, it appends ".causara_data".
- path (str): The file path where the data should be saved.
- Return: None
-
load(path)
Loads Real_World_Data from a file. It reads the file content and uses load_from_string() to reconstruct the data.
- path (str): The file path from which to load the data.
- Return: None
-
upload(key, name)
Uploads the Real_World_Data to the cloud using the specified key and name. The data is first converted to a string and then uploaded.
- key (str): The account key for authentication.
- name (str): The name under which the data will be stored (".causara_data" extension is appended if missing).
- Return: None
-
download(key, name)
Downloads Real_World_Data from the cloud using the provided key and name, then loads it into the current instance.
- key (str): The account key for authentication.
- name (str): The name under which the data is stored.
- Return: None
-
get(idx)
Retrieves the Data object at the specified index.
- idx (int): The index of the Data object to retrieve.
- Return: A Data object corresponding to the given index.
-
len()
Returns the number of Data objects stored.
- Return: An integer representing the total count of Data objects.
-
get_P()
Retrieves all problem instances (p) from the Data objects and returns them as a pandas DataFrame.
- Return: A pandas DataFrame where each row corresponds to a problem instance from a Data object.
-
get_X()
Retrieves the chosen solution (x) from each Data object and returns them as a pandas DataFrame.
- Return: A pandas DataFrame where each row contains the chosen solution from the corresponding Data object.
-
get_X_complete()
Retrieves the complete solution data (x_complete) from each Data object and returns it as a pandas DataFrame.
- Return: A pandas DataFrame containing all solution details for each Data object.
-
get_A()
Retrieves the alternatives from each Data object.
- Return: A list containing the alternatives for each Data object.
-
get_A_complete()
Retrieves the complete set of alternative solutions from each Data object.
- Return: A list of complete alternative solutions from each Data object.
-
get_Obj_X()
Retrieves the objective values for the chosen solution from each Data object.
- Return: A list of numeric objective values corresponding to the chosen solution of each Data object.
-
get_Obj_A()
Retrieves the objective values for the alternative solutions from each Data object.
- Return: A list of objective values for the alternative solutions from each Data object.
-
get_rw_Obj_X()
Retrieves the real-world objective values for the chosen solution from each Data object.
- Return: A list of real-world objective values (if provided) from each Data object.
Data
The Data class encapsulates a single real-world problem instance along with its computed solutions and associated metadata.
Each Data object stores the problem parameters (p), one or more solutions (list_of_x), a complete set of solution details (list_of_x_complete),
constant parameters (c and c_post), and additional information such as solving time, objective values, and model details.
-
set_rw_obj_value(rw_obj_value)
Sets the real-world objective value for the chosen solution.
- rw_obj_value (numeric): The real-world objective value.
- Return: None
-
set_chosen_idx(chosen_idx, user_explanation="")
Sets the index of the chosen solution along with an optional user explanation.
- chosen_idx (int): The index (0-based) of the chosen solution.
- user_explanation (str): An optional explanation from the user about why this solution was chosen.
- Return: None
-
get_rw_obj_value()
Retrieves the real-world objective value for the chosen solution.
- Return: A numeric value representing the real-world objective, or None if not set.
-
get_p()
Returns the problem instance stored in the Data object.
- Return: A dictionary representing the problem instance (p).
-
get_chosen_x()
Retrieves the chosen solution (x) from the list of solutions.
- Return: A dictionary containing the chosen solution. An error is raised if no solution has been chosen.
-
get_chosen_x_complete()
Retrieves the complete information for the chosen solution.
- Return: A dictionary with complete solution details.
-
export_chosen_x_to_JSON(path)
Exports the chosen solution to a JSON file at the specified path.
- path (str): The file path where the chosen solution should be saved.
- Return: None
-
get_obj_chosen_x()
Retrieves the objective value corresponding to the chosen solution.
- Return: A numeric value representing the objective value, or None if not available.
-
get_alternatives()
Retrieves all alternative solutions (x) excluding the chosen solution.
- Return: A list of dictionaries representing alternative solutions.
-
get_alternatives_complete()
Retrieves the complete information for all alternative solutions.
- Return: A list of dictionaries containing complete alternative solution details.
-
get_obj_alternatives()
Retrieves the objective values for all alternative solutions.
- Return: A list of numeric objective values for the alternatives.
-
set_endUserID(id)
Sets the identifier for the end user who provided the data.
- id (int or str): The end user identifier.
- Return: None
-
get_endUserID()
Returns the end user identifier.
- Return: An int or string representing the end user ID.
-
get_list_of_x()
Retrieves the list of chosen solutions (x) from the Data object.
- Return: A list of dictionaries representing the chosen solutions.
-
get_list_of_x_complete()
Retrieves the list of complete solutions (x_complete) from the Data object.
- Return: A list of dictionaries with full solution details.
-
get_model_name()
Returns the name of the model associated with this Data object.
- Return: A string representing the model name.
-
get_model_hash()
Retrieves the hash of the model used to generate this Data object.
- Return: A string representing the model hash.
-
get_model_version_nr()
Returns the version number of the model.
- Return: A string representing the model version.
-
get_date()
Retrieves the date when the Data object was created.
- Return: A string in ISO 8601 format representing the creation date.
-
get_solving_time()
Returns the time taken to solve the corresponding problem instance.
- Return: A numeric value (int or float) representing the solving time in seconds.
-
get_chosen_idx()
Returns the index of the chosen solution.
- Return: An integer indicating the chosen solution index, or None if not set.
-
set_user_explanation(explanation)
Sets an explanation provided by the user regarding the chosen solution.
- explanation (str): A textual explanation.
- Return: None
-
get_user_explanation()
Retrieves the user-provided explanation for the chosen solution.
- Return: A string containing the explanation.
Bounds
The Bounds class encapsulates the boundaries used to fine-tune constants.
-
add_relative_deviation_bound(key, min_ratio, max_ratio)
Adds a relative deviation bound for the constant named 'key'. The bound is defined as the interval from
min_ratio * initial_valuetomax_ratio * initial_value. For example, if the initial value provided in the c dict is 5.0 and themin_ratioandmax_ratioare 0.8 and 1.2 respectively, the optimization will be performed within the interval [4.0, 6.0].- key (str): The name of the constant to optimize
- min_ratio (float): Minimum relative deviation
- max_ratio (float): Maximum relative deviation
- Return: None
-
add_absolute_deviation_bound(key, min_deviation, max_deviation)
Adds an absolute deviation bound for the constant named 'key'. The bound is defined as the interval from
initial_value + min_deviationtoinitial_value + max_deviation. For example, if the initial value provided in the c dict is 5.0 and themin_deviationandmax_deviationare -0.5 and 0.5 respectively, the optimization will be performed within the interval [4.5, 5.5].- key (str): The name of the constant to optimize
- min_deviation (float): Minimum absolute deviation
- max_deviation (float): Maximum absolute deviation
- Return: None
 Learn a Gurobi Model from Data
Learn a Gurobi Model from Data